题目内容
4.已知y≠0,且2x2-9xy+8y2=0,则$\frac{4{x}^{2}-8xy-4{y}^{2}}{{x}^{2}+xy+3{y}^{2}}$的值为$\frac{20+20\sqrt{17}}{91+11\sqrt{17}}$或$\frac{20-20\sqrt{17}}{91-11\sqrt{17}}$.分析 已知等式变形,整理求出$\frac{x}{y}$的值,将已知等式变形表示出x2,代入原式化简,将$\frac{x}{y}$的值代入计算即可求出值.
解答 解:已知等式变形得:2×($\frac{x}{y}$)2-9×$\frac{x}{y}$+8=0,
解得:$\frac{x}{y}$=$\frac{9±\sqrt{17}}{4}$,
由2x2-9xy+8y2=0,得到x2=$\frac{9xy-8{y}^{2}}{2}$,
代入得:原式=$\frac{18xy-16{y}^{2}-8xy-4{y}^{2}}{\frac{9xy-8{y}^{2}}{2}+xy+3{y}^{2}}$=$\frac{20xy-40{y}^{2}}{11xy-2{y}^{2}}$=$\frac{20x-40y}{11x-2y}$=$\frac{20×\frac{x}{y}-40}{11×\frac{x}{y}-2}$,
当$\frac{x}{y}$=$\frac{9+\sqrt{17}}{4}$时,原式=$\frac{45+5\sqrt{17}-40}{\frac{99+11\sqrt{17}}{4}-2}$=$\frac{20+20\sqrt{17}}{91+11\sqrt{17}}$;
当$\frac{x}{y}$=$\frac{9-\sqrt{17}}{4}$时,原式=$\frac{45-5\sqrt{17}-40}{\frac{99-11\sqrt{17}}{4}-2}$=$\frac{20-20\sqrt{17}}{91-11\sqrt{17}}$.
故答案为:$\frac{20+20\sqrt{17}}{91+11\sqrt{17}}$或$\frac{20-20\sqrt{17}}{91-11\sqrt{17}}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

 寒假学与练系列答案
寒假学与练系列答案| A. | (x+2)(x-6) | B. | (x-2)(x+6) | C. | (x+3)(x-4) | D. | (x-3)(x+4) |
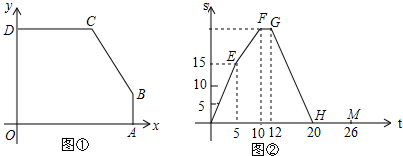
 如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿平移,阴影部分的面积为140cm2.
如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿平移,阴影部分的面积为140cm2.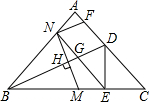 如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )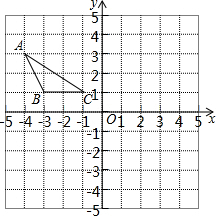 如图,△ABC在下列网格中,BC=2,BC∥x轴,B点坐标(-3,1),点A坐标是(-4,3)
如图,△ABC在下列网格中,BC=2,BC∥x轴,B点坐标(-3,1),点A坐标是(-4,3)