题目内容

16．甲、乙两地高速公路全长420千米，一辆小汽车和一辆客车同时从甲、乙两地相向开来，经过2.5小时相遇，相遇时，小汽车比客车多行驶70千米，求小汽车和客车的平均速度．

分析 设相遇时客车行驶了x千米，则小汽车行驶了（x+70）千米，根据路程=客车行驶的路程+小汽车行驶的路程即可得出关于x的一元一次方程，解之即可得出x的值，再根据速度=路程÷时间即可求出小汽车和客车的平均速度．

解答 解：设相遇时客车行驶了x千米，则小汽车行驶了（x+70）千米，
根据题意得：x+x+70=420，
解得：x=175，
∴x+70=245．
175÷2.5=70（千米/小时），
245÷2.5=98（千米/小时）．
答：小汽车的平均速度为98千米/小时，客车的平均速度为70千米/小时．

点评 本题考查了一元一次方程的应用，根据路程=客车行驶的路程+小汽车行驶的路程列出关于x的一元一次方程．

练习册系列答案
相关题目
6．已知点（4，5）于点B（m，n）关于原点O对称，则m的值为（　　）
A．-4B．4C．-5D．5
7．已知AB=8，从12，10两个数中任取一个数作为AC的长，从10，8，6，4中任取一个数作为BD的长，经过恰当摆放，总会摆出四边形ABCD，如果对角线分别相同的四边形算作同一种四边形，那么四边形ABCD是平行四边形的概率是$\frac{5}{8}$．
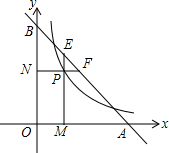4．如图，直线y=6-x交x轴、y轴于A、B两点，P是反比例函数y=$\frac{k}{x}$（x＞0）图象上位于直线下方的一点，过点P作x轴的垂线，垂足为点M，交AB于点E，过点P作y轴的垂线，垂足为点N，交AB于AB于点F，且AF•BE=8，则k=4．
11．如图，A、B两点分别位于一个池塘的两端，小明想用绳子测量A，B的距离，但绳子不够，一位同学帮他想了一个主意：先在地上取一个可以直接达到A的点C，找到AC，BC的中点D，E，并且量得DE的长为15米，则A，B两点间的距离是（　　）
A．15米B．20米C．30米D．40米
1．如图1，已知抛物线y=a（x2-2mx-3m2）（a＞0，m＞0）交x轴于A、B两点（点A在点B的左侧）．交y轴于点C．

（1）若m=1．求AB的长度；
（2）若a=1，m=1，P是对称轴右侧抛物线上的点．当∠ACP=∠ABC时，求P点坐标；
（3）如图2．当am=1时．点N（0，n）在y轴负半轴上（点N在点C下方），直线NB交抛物线于另一点D，直线NA交抛物线于另一点E，作EM⊥x轴于M．若$\frac{ND}{BD}$=$\frac{1}{2}$．试判断$\frac{EM}{ON}$是否为定值？若是，求出该定值；若不是，说明理由．
8．如图，一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P，Q两点，对于函数y3═ax2+（b-1）x+c，有下列结论：
①a+c＞0；②b＜1；③函数y3的图象与x轴的两个交点都在正半轴上；
其中，正确结论的个数是（　　）
A．0个B．1个C．2个D．3个
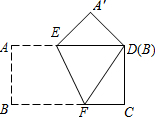5．把一张矩形纸片ABCD按如图所示的方式折叠，使顶点B和D重合，折痕为EF．
（1）求证：△A′DE≌△DCF．
（2）若BC=8，AB=4，求AE的长．
（3）若BC=8，AB=4，求折痕EF的长．
6．使二次根式$\sqrt{x-2}$有意义的x的取值范围是（　　）
A．x＞2B．x≥2C．x＜2D．x＞-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网