题目内容
7.已知AB=8,从12,10两个数中任取一个数作为AC的长,从10,8,6,4中任取一个数作为BD的长,经过恰当摆放,总会摆出四边形ABCD,如果对角线分别相同的四边形算作同一种四边形,那么四边形ABCD是平行四边形的概率是$\frac{5}{8}$.分析 画树状图展示所有8种等可能的结果数,由于对角线分别相同的四边形算作同一种四边形,利用对角线互相平分的四边形为平行四边形和三角形三边的关系可判断四边形ABCD是平行四边形的结果数为5,然后根据概率公式求解.
解答 解:画树状图为:
共有8种等可能的结果数,其中四边形ABCD是平行四边形的结果数为5,
所以四边形ABCD是平行四边形的概率=$\frac{5}{8}$.
故答案为$\frac{5}{8}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
18.下列计算中,正确的是( )
| A. | (-xy)3=-xy3 | B. | (2x2y)2=2x4y2 | C. | ($\frac{2}{3}$x2y)2=$\frac{3}{4}$x4y2 | D. | ($\frac{1}{3}$xy2)3=$\frac{1}{27}$x3y6 |
12.当x≠0时,下列运算不正确的是( )
| A. | a2•a=a3 | B. | (-a3)2=a6 | C. | (3a2)2=9a4 | D. | a3÷a3=a |
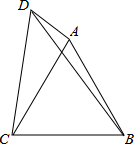 如图,在四边形ABCD中,△ABC是等边三角形,∠ADC=∠ABC,若AD=3,BC=7,则线段BD的长为$\sqrt{97}$.
如图,在四边形ABCD中,△ABC是等边三角形,∠ADC=∠ABC,若AD=3,BC=7,则线段BD的长为$\sqrt{97}$. 如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?
如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗? 如图,△ABC中,AC=BC,∠ACB=90°,点D是AB上一点,∠ACD=15°,点B、点E关于CD对称,连BE交CD于点H,交AC于点G,连DE交AC于点F.则∠ADF=60°.
如图,△ABC中,AC=BC,∠ACB=90°,点D是AB上一点,∠ACD=15°,点B、点E关于CD对称,连BE交CD于点H,交AC于点G,连DE交AC于点F.则∠ADF=60°.


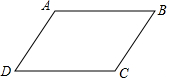 如图,AB∥CD,AD∥BC,说明∠B=∠D的理由.
如图,AB∥CD,AD∥BC,说明∠B=∠D的理由.