题目内容
18．分解因式：（1）p2（p-q）+（q-p）；
（2）（a2+b2）2-4a2b2；
（3）（x-y）2-4（x-y-1）．
分析 （1）原式变形后提取公因式，再利用平方差公式分解即可；
（2）原式利用平方差公式化简，再利用完全平方公式分解即可；
（3）原式整理后利用完全平方公式分解即可．
解答 解：（1）原式=p2（p-q）-（p-q）=（p-q）（p+1）（p-1）；
（2）原式=（a2+b2+2ab）（a2+b2-2ab）=（a+b）2（a-b）2；
（3）原式=（x-y）2-4（x-y）+4=（x-y-2）2．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
8．一元二次方程3x2-8x-10=0的二次项是（ ）
| A． | 3x2 | B． | 3 | C． | -8x | D． | -8 |
10．在△ABC中，AB=8，∠ABC=30°，AC=5，则BC的长为（ ）
| A． | 4$\sqrt{3}$ | B． | 4$\sqrt{3}$+3 | C． | 4$\sqrt{3}$-3 | D． | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
7．用反证法证明命题：在一个三角形中，至少有一个内角不大于60°．证明的第一步是（ ）
| A． | 假设三个内角都不大于60° | B． | 假设三个内角都大于60° | ||
| C． | 假设三个内角至多有一个大于60° | D． | 假设三个内角至多有两个大于60° |
8．
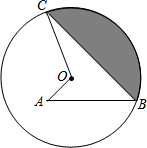如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）
如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）| A． | $\frac{4π}{3}$+2$\sqrt{3}$ | B． | $\frac{2π}{3}$+2$\sqrt{3}$ | C． | $\frac{4π}{3}$+$\sqrt{3}$ | D． | $\frac{2π}{3}$+$\sqrt{3}$ |