题目内容
15.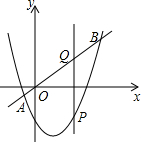 如图所示,直线y=x与抛物线 y=x2-x-3交于A,B两点,点P是抛物线上的一个动点,点P作PQ⊥x轴交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随着m的增大而减小时m的取值范围是m<-1或1<m<3.
如图所示,直线y=x与抛物线 y=x2-x-3交于A,B两点,点P是抛物线上的一个动点,点P作PQ⊥x轴交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随着m的增大而减小时m的取值范围是m<-1或1<m<3.
分析 可用m分别表示出P、Q的坐标,则可用m表示出PQ的长,再利用二次函数的性质可求得答案.
解答 解:
联立直线和抛物线解析式可得$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}-x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴A(-1,-1),B(3,3),
∵点P在抛物线上,点Q在直线y=x上,且点P的横坐标为m,
∴P(m,m2-m-3),Q(m,m),
当m<-1或m>3时,可知点P在点Q上方,
∴PQ=m2-m-3-m=m2-2m+4=(m-1)2-4,
∴当m<1时PQ的长度随m的增大而减小;
当-1<m<3时,可知点Q在点P上方,
∴PQ=m-(m2-m-3)=-m2+2m+3=-(m-1)2+4,
此时抛物线开口向下,对称轴为m=1,
∴当1<m<3时,PQ随m的增大而减小,
综上可知m的取值范围为:m<-1或1<m<3,
故答案为:m<-1或1<m<3.
点评 本题主要考查二次函数的性质,利用m表示出PQ的长度是解题的关键,注意分类讨论.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
2.去年10月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市500名初中学生坐姿、站姿、走姿的好坏情况,数据如表:
我们要想知道每种形体占所抽查总人数的百分比,需对专家的测评数据作适当处理,画出适当的统计图,应选择什么统计图呢?
| 坐姿不良 | 站姿不良 | 走姿不良 | 三姿良好 |
| 100 | 155 | 185 | 60 |
20.公园门票价格规定如表:
某学校七年级(1)、(2)两个班共104人去游公园,其中(1)班人数较少,多于4人,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才能省钱?省多少?
| 购票张数 | 1-50张 | 51~100张 | 100张以上 |
| 每张票价 | 13元 | 11元 | 9元 |
(1)两班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才能省钱?省多少?
5.先填表,通过观察后再回答问题
(1)被汗方数a的小数点位置移动和它的算术平方根$\sqrt{a}$的小数点位置移动有无规律?若有规律,请写出它的移动规律;
(2)已知:$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(3)试比较$\sqrt{a}$与a的大小.
| a | … | 0.000001 | 0.0001 | 0.01 | 1 | 100 | 10000 | 100000 | … |
| $\sqrt{a}$ | … | … |
(2)已知:$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(3)试比较$\sqrt{a}$与a的大小.