题目内容
1. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
分析 先由折叠得出CE=AE=4-AE,再用勾股定理求解即可.
解答 解:如图,连接CE,
∵四边形ABCD是矩形,
∴∠B=90°,
由折叠得,CE=AE,
∵AB=AE+BE=4,
∴CE=AE=4-BE,
在Rt△BCE中,BC=2,
∴CE2-BE2=BC2,
∴(4-BE)2-BE2=4,
∴BE=$\frac{3}{2}$,
故选B.
点评 此题主要考查了图形的翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
16.两个数的商为正数,则两个数( )
| A. | 都为正 | B. | 都为负 | C. | 同号 | D. | 异号 |
 如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?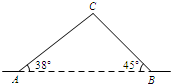 如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)
如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)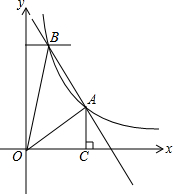 如图,在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$(m≠0,x>0)的图象交于第一象限内的A、B两点,过点A作AC⊥x轴于点C,AC=3,点B的坐标为(2,6)
如图,在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$(m≠0,x>0)的图象交于第一象限内的A、B两点,过点A作AC⊥x轴于点C,AC=3,点B的坐标为(2,6)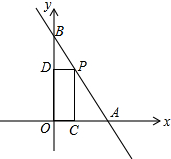 如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D.
如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D.