题目内容
2.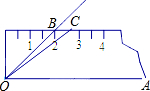 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 过点B作BD⊥OA于D,过点C作CE⊥OA于E.首先在等腰直角△BOD中,得到BD=OD=2cm,则CE=2cm,然后在直角△COE中,根据正切函数的定义即可求出OE的长度.
解答  解:过点B作BD⊥OA于D,过点C作CE⊥OA于E.
解:过点B作BD⊥OA于D,过点C作CE⊥OA于E.
在△BOD中,∠BDO=90°,∠DOB=45°,
∴BD=OD=2cm,
∴CE=BD=2cm.
在△COE中,∠CEO=90°,∠COE=37°,
∵tan37°=$\frac{CE}{OE}$≈0.75,∴OE≈2.7cm.
∴OC与尺上沿的交点C在尺上的读数约为2.7cm.
故答案为2.7.
点评 本题考查了解直角三角形的应用,属于基础题型,难度中等,通过作辅助线得到CE=BD=2cm是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
10.计算(-2a2)3的结果等于( )
| A. | -2a5 | B. | -8a5 | C. | -2a6 | D. | -8a6 |
17.一个角的余角是它的3倍,则这个角的度数是( )
| A. | 22.5° | B. | 25° | C. | 30° | D. | 20.5° |
12.若a+$\frac{1}{a}$=2,则a2+$\frac{1}{{a}^{2}}$的值为( )
| A. | 2 | B. | 4 | C. | 0 | D. | -4 |