题目内容
8.(1)如图1,在△ABC中,AD平分∠BAC交BC于点D,求证:CD:BD=AC:AB.证明:过点A作AG⊥BC于点G,过点D分别作DE⊥AC于点E,DF⊥AB于点F.请完成后面的证明;(2)如图2,在菱形ABCD中,点E是AB的中点,连接DE交AC于点F,直接利用(1)的结论求AF:FC.

分析 (1)根据角平分线的性质得到DE=DF,根据三角形的面积公式证明即可;
(2)根据菱形的性质得到AB∥CD,根据相似三角形的判定定理得到△AEF∽△DCF,根据相似三角形的性质计算即可.
解答 (1)证明:过点A作AG⊥BC于点G,过点D分别作DE⊥AC于点E,DF⊥AB于点F,
∵AD平分∠BAC,DE⊥AC,DF⊥AB,
∴DE=DF,
△ADC的面积=$\frac{1}{2}$×AC×DE=$\frac{1}{2}$×CD×AG,
△ADB的面积=$\frac{1}{2}$×AB×DF=$\frac{1}{2}$×BD×AG,
∴CD:BD=AC:AB;
(2)解:∵四边形ABCD为菱形,
∴AB∥CD,AB=CD,
∴△AEF∽△DCF,
∴AE:CD=AF:FC,
∴AF:FC=1:2.
点评 本题考查的是角平分线的性质、相似三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13.下列计算正确的是( )
| A. | 25+25=26 | B. | x3+x3=x6 | C. | (2x3)2=4x9 | D. | (3x3)2=6x6 |
17.下列运算中错误的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{3}$×$\sqrt{2}$=6 | C. | $\sqrt{8}$÷$\sqrt{2}$=2 | D. | (-$\sqrt{3}$)2=3 |
18.已知y=x2+(t-2)x-2,当x>1时y随x的增大而增大,则t的取值范围是( )
| A. | t>0 | B. | t=0 | C. | t<0 | D. | t≥0 |
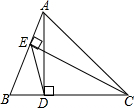 如图,在△ABC中,AD、CE分别为BC、AB边上的高,且AD为12厘米,S△AED:S△ABC=1:4,求BD的长.
如图,在△ABC中,AD、CE分别为BC、AB边上的高,且AD为12厘米,S△AED:S△ABC=1:4,求BD的长.