题目内容
16.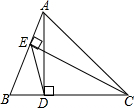 如图,在△ABC中,AD、CE分别为BC、AB边上的高,且AD为12厘米,S△AED:S△ABC=1:4,求BD的长.
如图,在△ABC中,AD、CE分别为BC、AB边上的高,且AD为12厘米,S△AED:S△ABC=1:4,求BD的长.
分析 根据已知条件得到A、C、D、E四点共圆,根据圆内接四边形的性质得到∠BDE=∠BAC,推出△BDE∽△BAC,根据相似三角形的性质得到$\frac{BD}{BA}$=$\frac{1}{2}$,根据勾股定理即可得到结论.
解答 解:∵AD、CE分别为BC、AB边上的高,
∴A、C、D、E四点共圆,
∴∠BDE=∠BAC,
∵∠B=∠B,
∴△BDE∽△BAC,
∵S△AED:S△ABC=1:4,
∴$\frac{BD}{BA}$=$\frac{1}{2}$,
∴AB=2BD,
在Rt△ABD中,∵AD=12cm
∴根据勾股定理得AB2-BD2=144,
∴3BD2=144,
∴BD=4$\sqrt{3}$.
点评 本题考查了三角形的面积,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
7.点P在第四象限且到x轴的距离为4,到y轴的距离为5,则P点的坐标是( )
| A. | (4,-5) | B. | (-4,5) | C. | (-5,4) | D. | (5,-4) |
11.下列运算正确的是( )
| A. | (a2b)3=a6b3 | B. | (a2)3=a8 | C. | a6÷a2=a3 | D. | a2•a3=a6 |
5.下列四个数中,最小的是( )
| A. | 0 | B. | -2 | C. | -8 | D. | 1 |
6.下列计算错误的是( )
| A. | (-$\frac{2}{3}$)2=$\frac{4}{6}$ | B. | (-$\frac{3}{4}$)2=$\frac{9}{16}$ | C. | -(-$\frac{2}{5}$)2=-$\frac{4}{25}$ | D. | 02016=0 |
