题目内容
1.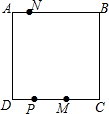 如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?
如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?
分析 因为90、120、60和80的最小公倍数是720,所以设正方形的边长为720千米,由此可以求出AB、BC、CD、DA分别需要多少小时,进而求出两车在AB上相遇所用时间,再求出AN、NB各需要的时间,然后求出它们距离的比.
解答 解:设正方形的边长为720千米,
AB、BC、CD和DA分别需要8,6,12,9小时,
D→P需要(12-9+6)÷2=4.5(小时),
P→D→A需要13.5小时,这时相距8+6-13.5=0.5小时的路程,
A→N就需要0.5÷2=0.25(小时),
N→B需要8-0.25=7.75(小时),
所以AN:NB=0.25:8=1:32;
答:AN的距离和NB距离的比是1:31.
点评 此题解答关键是求出汽车在正方形ABCD各边上所以的时间,进而求出AN、NB各需要的时间,问题便得到解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列说法属于不可能事件的是( )
| A. | 四边形的内角和为360° | B. | 梯形的对角线不相等 | ||
| C. | 内错角相等 | D. | 存在实数x满足x2+1=0 |
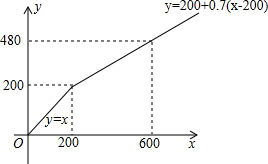 甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.
甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.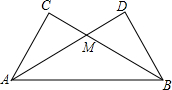 把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明:
把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明: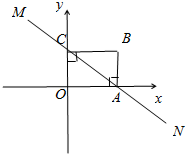 直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.
直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.