题目内容
13.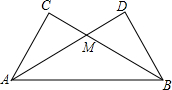 把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明:
把两个同样大小的含30度的三角尺像如图所示那样放置,其中M是AD与BC的交点.证明:(1)MC的长度等于点M到AB的距离;
(2)求∠AMB的度数.
分析 (1)利用角平分线的性质以及全等三角形的性质得出答案;
(2)由三角形内角和定理直接得出.
解答 (1)证明:过点M做MN⊥AB,
由题意可得:∠CAD=∠DAB=30°,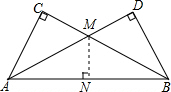
∵∠C=90°,MN⊥AB,
∴MC=MN(角平分线上的点到角的两边距离相等),
则MC的长度就等于点M到AB的距离.
(2)解:由题意知:∠MAB=∠MBA=30°,
∴∠AMB=180°-30°-30°=120°.
点评 此题主要考查了角的平分线的性质的应用三角形的内角和定理,熟练应用角平分线的性质是解题关键.

练习册系列答案
相关题目
4.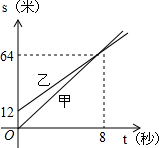 如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
 如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
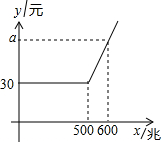 某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位:兆)的函数关系的图象如图所示.若该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,则图中a的值为59.
某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位:兆)的函数关系的图象如图所示.若该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,则图中a的值为59.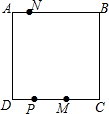 如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?
如图所示,正方形ABCD是一条环行公路,已知汽车在AB上的时速为90千米,在BC上的时速为120千米,在CD上的时速为60千米,在DA上的时速为80千米,从DC上一点P同时反向各出发一辆汽车它们将在AB上的中点相遇;如果PC的中点M处各发出一辆汽车,它们将在AB上一点N相遇,那么A到N的距离是N到B距离的几倍?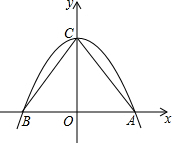 如图,抛物线y=-x2+4交x轴于A、B两点,顶点为C.
如图,抛物线y=-x2+4交x轴于A、B两点,顶点为C.