Question

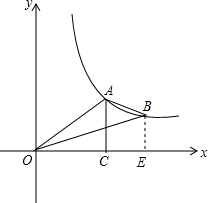如图，点A、B在反比例函数y=

k

x

的图象上，且点A、B的横坐标分别为a、2a（a＞0），AC⊥x轴，垂足为点C，且△AOC的面积为2；
（1）求该反比例函数的解析式；
（2）连接AB，过点B作BE⊥x轴，交x轴于点E，求四边形OABE的面积．

Answer 1

考点：待定系数法求反比例函数解析式,反比例函数系数k的几何意义

专题：

分析：（1）由S_△AOC=

1

2

xy=2，设反比例函数的解析式y=

k

x

，则k=xy=4；
（2）连接AB，过点B作BE⊥x轴，交x轴于E点，通过分割面积法S_△AOB=S_△AOC+S_梯形-S_△BOE求得．

解答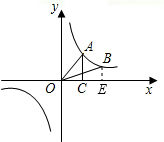：解：（1）∵S_△AOC=2，
∴k=2S_△AOC=4；
∴y=

4

x

；

（2）连接AB，过点B作BE⊥x轴，
S_△AOC=S_△BOE=2，
∴A（a，

4

a

），B（2a，

2

a

）；
S_梯形ACEB=

1

2

（

4

a

+

2

a

）×（2a-a）=3，
∴S_△AOB=S_△AOC+S_梯形ACEB-S_△BOE=3．

点评：此题考查了待定系数法求反比例函数解析式，反比例函数系数k的几何意义．重点考查了函数性质的应用和图形的分割转化思想．同学们要熟练掌握这类题型．