题目内容
11. 如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).
如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).
分析 利用位似图形的性质结合已知点的坐标得出$\frac{PO}{PA}$=$\frac{DO}{AB}$,进而求出P点坐标.
解答 解:∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),
∴D(0,1),B(4,2),
∴$\frac{PO}{PA}$=$\frac{DO}{AB}$,
则$\frac{PO}{PO+4}$=$\frac{1}{2}$,
解得:OP=4,
则点P的坐标为:(-4,0).
故答案为:(-4,0).
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于一点,则这个正比例函数的表达式是( )
如图,一个正比例函数图象与一次函数y=-x+1的图象相交于一点,则这个正比例函数的表达式是( )
 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于一点,则这个正比例函数的表达式是( )
如图,一个正比例函数图象与一次函数y=-x+1的图象相交于一点,则这个正比例函数的表达式是( )| A. | y=-2x | B. | y=2x | C. | y=$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x |
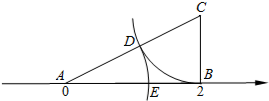 如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是$\sqrt{5}$-1.
如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是$\sqrt{5}$-1. 如图,点O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC
如图,点O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6.
一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6. 如图,圆锥体的高h=$\sqrt{3}$cm,底面半径r=1cm,则圆锥体的侧面积为2πcm2.
如图,圆锥体的高h=$\sqrt{3}$cm,底面半径r=1cm,则圆锥体的侧面积为2πcm2.