题目内容
11．“三角形中至少有一个内角大于等于60°”，这个命题用反证法证明应假设三角形中三个内角都小于60°．分析 熟记反证法的步骤，从命题的反面出发假设出结论，直接填空即可．
解答 解：∵三角形中至少有一个内角大于等于60°，
∴第一步应假设结论不成立，
即三角形中三个内角都小于60°．
故答案为：三角形中三个内角都小于60°．
点评 此题主要考查了反证法，反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．在假设结论不成立时，要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
练习册系列答案
相关题目
19．
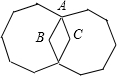如图，平面上有两个全等的正八边形，∠BAC为（ ）
如图，平面上有两个全等的正八边形，∠BAC为（ ）| A． | 60° | B． | 45° | C． | 30° | D． | 72° |
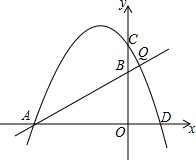设直线y=$\frac{1}{2}$x+2与抛物线y=-$\frac{1}{2}$x2-x+4交于点A，点Q，若在x轴上方的抛物线上只存在相异的两点M、N，S△MAQ=S△NAQ=S，则S的取值范围$\frac{15}{2}$＜S＜$\frac{125}{16}$．
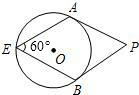如图，点E是半径为6的⊙O上一点，过点E作一只60°的圆周角∠AEB，分别过点A、B作⊙O的切线，两条切线交于点P．那么四边形AEBP的面积的最大值是54$\sqrt{3}$．
3．函数y=$\frac{3}{x}$与y=x-1图象的一个交点的横、纵坐标分别为a、b，则$\frac{1}{a}$-$\frac{1}{b}$的值为（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | 3 | D． | 1-3 |
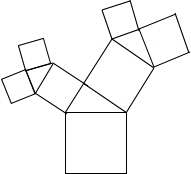如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则所有正方形的面积的和是（ ）cm2．