题目内容
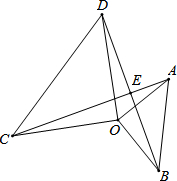 如图,等腰直角△AOB与等腰直角△COD有公共顶点O,点C、O、B不在同一条直线上,求证:
如图,等腰直角△AOB与等腰直角△COD有公共顶点O,点C、O、B不在同一条直线上,求证:(1)AC=BD;
(2)AC⊥BD.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)由三角形AOB与三角形COD为等腰直角三角形,得到一对角相等,利用等式的性质得到夹角相等,利用SAS得到三角形AOC与三角形BOD全等,利用全等三角形对应边相等即可得证;
(2)由(1)全等三角形对应角相等得到∠ACO=∠BDO,设AC与OD交于点F,利用等角的余角相等得到∠DEF=90°,即可得证.
(2)由(1)全等三角形对应角相等得到∠ACO=∠BDO,设AC与OD交于点F,利用等角的余角相等得到∠DEF=90°,即可得证.
解答: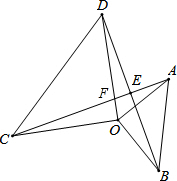 证明:(1)∵△AOB与△COD为等腰直角三角形,
证明:(1)∵△AOB与△COD为等腰直角三角形,
∴∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)∵△AOC≌△BOD,
∴∠ACO=∠BDO,
令AC交DO于F点,
又∵∠COD=90°,
∴∠ACO+∠CFO=90°,
又∵∠CFO=∠DFE,
∴∠BDO+∠DFE=90°,即∠DEF=90°,
则AC⊥BD.
 证明:(1)∵△AOB与△COD为等腰直角三角形,
证明:(1)∵△AOB与△COD为等腰直角三角形,∴∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)∵△AOC≌△BOD,
∴∠ACO=∠BDO,
令AC交DO于F点,
又∵∠COD=90°,
∴∠ACO+∠CFO=90°,
又∵∠CFO=∠DFE,
∴∠BDO+∠DFE=90°,即∠DEF=90°,
则AC⊥BD.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若0<x<1时,比较x,
,x2的大小( )
| 1 |
| x |
A、x<
| ||
B、
| ||
C、x2<
| ||
D、x2<x<
|
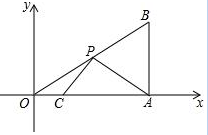 如图,Rt△OAB的直角顶点A在x轴的正半轴上,∠AOB=30°,B(6,
如图,Rt△OAB的直角顶点A在x轴的正半轴上,∠AOB=30°,B(6,

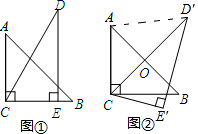 一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D′CE′(如图②),此时AB与CD′交于点O,则cos∠OAD′=
一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D′CE′(如图②),此时AB与CD′交于点O,则cos∠OAD′=