题目内容
8.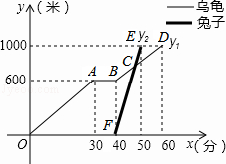 “龟兔首次赛跑”后输了比赛的兔子没有气馁,总结反思后,决定和乌龟再赛一次,图中折线反映了第二次比赛的故事.(x表示乌龟从起点出发所行时间y1,为乌龟的行程路,y2为兔子的行程路)
“龟兔首次赛跑”后输了比赛的兔子没有气馁,总结反思后,决定和乌龟再赛一次,图中折线反映了第二次比赛的故事.(x表示乌龟从起点出发所行时间y1,为乌龟的行程路,y2为兔子的行程路)①第二次赛跑的总路程为1000m;
②乌龟先出发40分钟;
③途中乌龟休息了10分钟;
④兔子在途中几百米处追上乌龟.
分析 ①由函数图象的纵坐标,即可解答;②根据函数图象的横坐标,即可解答;③根据函数图象的横坐标,即可解答;④根据函数图象的交点,可判断.
解答 解:根据图象可知:
①龟兔再次赛跑的路程为1000米,故答案为:1000;
②兔子在乌龟跑了40分钟之后开始跑,故答案为:40;
③乌龟在30--40分钟时的路程为0,故这10分钟乌龟没有跑在休息,故答案为:10;
④由函数图象可得:y1=20x-200(40≤x≤60),y2=100x-4000(40≤x≤50),
当y1=y2时,兔子追上乌龟,
此时20x-200=100x-4000,
解得:x=47.5,
y1=y2=750米,即兔子在途中750米处追上乌龟.
点评 本题考查了函数图象,观察函数图象的横坐标得出时间,函数图象的纵坐标得出路程是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
17. 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )| A. | 当x=2时,y=5 | B. | 矩形MNPQ的面积是20 | ||
| C. | 当x=6时,y=10 | D. | 当y=$\frac{15}{2}$时,x=10 |

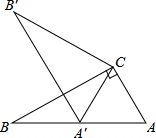 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为60°.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为60°.