题目内容
18.平面上有n个点(n≥3),任意三点不在同一直线上,过任意三点作三角形,一共能作多少个不同的三角形?(1)分析:当有3个点时,可作1个三角形;
当有4个点时,可作4个三角形;
当有5个点时,可作10个三角形…
(2)归纳:点的个数n和可以作出三角形的个数Sn的关系为$\frac{n(n-1)(n-2)}{6}$.
分析 顺次连接不在同一直线上的三个点可作1个三角形;当有4个点时,可作4个三角形;当有5个点时,可作10个三角形;依此类推当有n个点时,可作$\frac{n(n-1)(n-2)}{6}$个三角形.
解答 解:当n=3时,可作出的三角形的个数S3=$\frac{3×2×1}{6}$=1;
当n=4时,可作出的三角形的个数S4=$\frac{4×3×2}{6}$=4;
当n=5时,可作出的三角形的个数S5=$\frac{5×4×3}{6}$=10;
当点的个数是n时,可作出的三角形的个数Sn=$\frac{n(n-1)(n-2)}{6}$.
∴Sn=$\frac{n(n-1)(n-2)}{6}$.
(1)故答案为:1,4,10;
(2)故答案为:$\frac{n(n-1)(n-2)}{6}$.
点评 此题考查了规律总结,运用由特殊到一般的方法,进行归纳总结,解题的关键是能够得到三角形个数与n的值的通项公式,难度不大.

练习册系列答案
相关题目
6.若关于x的一元二次方程(k+1)x2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-2,且k≠-1 | B. | k>-2 | C. | k<-2 | D. | k为任意实数 |
3.一种面粉的质量标识为“30±0.2千克”,则下列面粉中合格的是( )
| A. | 29.2千克 | B. | 29.9千克 | C. | 30.5千克 | D. | 32.2千克 |
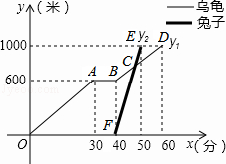 “龟兔首次赛跑”后输了比赛的兔子没有气馁,总结反思后,决定和乌龟再赛一次,图中折线反映了第二次比赛的故事.(x表示乌龟从起点出发所行时间y1,为乌龟的行程路,y2为兔子的行程路)
“龟兔首次赛跑”后输了比赛的兔子没有气馁,总结反思后,决定和乌龟再赛一次,图中折线反映了第二次比赛的故事.(x表示乌龟从起点出发所行时间y1,为乌龟的行程路,y2为兔子的行程路) 如图所示,已知AD平分∠CAE,∠B=∠1,证明:AD∥BC.
如图所示,已知AD平分∠CAE,∠B=∠1,证明:AD∥BC.