题目内容
7.已知y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,得到图象的解析式为y=x2-2x-3.(1)求b,c的值;
(2)写出原函数图象的顶点坐标、对称轴方程和函数的最小值.
分析 (1)利用二次函数平移的性质得出平以前的函数解析式;
(2)利用配方法求出二次函数的顶点坐标和最值即可.
解答 解:(1)∵y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,得到图象的解析式为y=x2-2x-3,
∴y=x2-2x-3=(x-1)2-4,向左平移2个单位,向上平移3个单位后得到:y=(x+1)2-1=x2+2x,
故b=2,c=0;
(2)由(1)得:原函数图象的顶点坐标为:(-1,-1),
对称轴方程为:直线x=-1;
函数的最小值为:-1.
点评 此题主要考查了二次函数图象与几何变换以及配方法求二次函数最值,正确掌握配方法求二次函数顶点坐标是解题关键.

练习册系列答案
相关题目
13.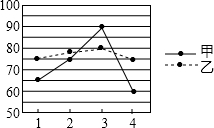 如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )
如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )
 如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )
如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )| A. | 甲成绩比乙成绩稳定 | B. | 乙成绩比甲成绩稳定 | ||
| C. | 甲、乙两成绩一样稳定 | D. | 不能比较两人成绩的稳定性 |
 如图,B、A、E在同一条直线上,则∠CAD+∠B+∠C+∠D+∠E=180°.
如图,B、A、E在同一条直线上,则∠CAD+∠B+∠C+∠D+∠E=180°.