题目内容
已知x=4满足方程x2-
mx=m2,试求出所有满足该方程的x和m的值.
| 3 |
| 2 |
考点:一元二次方程的解
专题:
分析:把x=4代入已知方程,列出关于m的新方程,通过解方程求得m的值;然后利用根与系数的关系来求方程的另一根.
解答:解:设方程的另一根为a.
依题意得
42-
×4m=m2,即(m+8)(m-2)=0,
解得 m1=-8,m2=2.
当m=-8时,4a=-(-8)2,解得a=-16.
当m=2时,4a=-22,解得 a=-1.
综上所述,满足方程的另外两根是-16或-1.所对应的m的值是-8、2.
依题意得
42-
| 3 |
| 2 |
解得 m1=-8,m2=2.
当m=-8时,4a=-(-8)2,解得a=-16.
当m=2时,4a=-22,解得 a=-1.
综上所述,满足方程的另外两根是-16或-1.所对应的m的值是-8、2.
点评:本题考查了一元二次方程的解的定义.此题利用根与系数的关系求得方程的另一根.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
如果两个圆的半径分别为4cm和5cm,圆心距为1cm,那么这两个圆的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
 如图:在△ABC中,∠BAC=100°,∠ACB=20°,CE是∠ACB的角平分线,D是BC上一点,若∠DAC=20°,求∠CED的度数.
如图:在△ABC中,∠BAC=100°,∠ACB=20°,CE是∠ACB的角平分线,D是BC上一点,若∠DAC=20°,求∠CED的度数.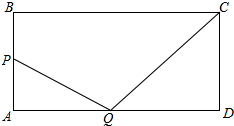 如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值.
如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值.