题目内容
3.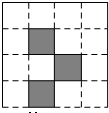 如图,在4×4的正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4的正方形网格中,任选一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{13}$ |
分析 由在4×4正方形网格中,任选取一个白色的小正方形并涂黑,共有16种等可能的结果,使图中黑色部分的图形构成一个轴对称图形的有5种情况,直接利用概率公式求解即可求得答案.
解答 解:∵由题意,共16-3=13种等可能情况,其中构成轴对称图形的有如下5个图所示的5种情况,
∴
概率为P=$\frac{5}{13}$.
∴选D.
点评 本题考查了利用列表法与树状图法求概率的方法:先列表展示所有等可能的结果数n,再找出某事件发生的结果数m,然后根据概率的定义计算出这个事件的概率=$\frac{m}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.2cos60°的值是( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
11.下列实数中,是有理数的为( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{21}$ | C. | sin45° | D. | π |
18.在实数-0.8,2015,-$\frac{22}{7}$,$\frac{\sqrt{3}}{3}$四个数中,是无理数的是( )
| A. | -0.8 | B. | 2015 | C. | -$\frac{22}{7}$ | D. | $\frac{\sqrt{3}}{3}$ |
12.对点(x,y)的一次操作变换记为p1(x,y),定义其变换法则如下:p1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).例如:p1(1,2)=(3,-1),p2(1,2)=p1(p1(1,2))=p1(3,-1)=(2,4),p3(1,2)=p1(p2(1,2))=p1(2,4)=(6,-2).则p2014(1,-1)=( )
| A. | (0,21006) | B. | (21007,-21007) | C. | (0,-21006) | D. | (21006,-21006) |
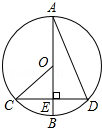 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为10.
如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为10.