题目内容
20.用适当的方法解方程:(x-1)2=3(x-1).分析 方程移项变形后,利用因式分解法求出解即可.
解答 解:方程整理得:(x-1)2-3(x-1)=0,
分解因式得:(x-1)(x-1-3)=0,
解得:x=1或x=4.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
8.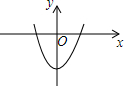 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
15.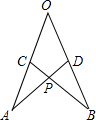 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )
如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )
①△AOD≌△BOC;②△APC≌△BPD;③PC=PD.
 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )
如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )①△AOD≌△BOC;②△APC≌△BPD;③PC=PD.
| A. | ①②③ | B. | ①② | C. | ② | D. | ① |
9.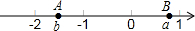 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
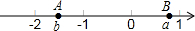 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
10. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )| A. | $\sqrt{23}$ | B. | $\sqrt{13}$ | C. | $\sqrt{17}$ | D. | $\sqrt{26}$ |
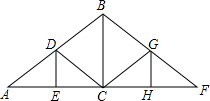 如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=12m,∠A=30°,则DE等于3.
如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=12m,∠A=30°,则DE等于3. 已知:如图,△OAB,分别画出与△OAB关于x轴、y轴对称的图形△OA1B1和△OA2B2,△OA1B1和△OA2B2各顶点的坐标为O(0,0)、A1(1,-3)、B1(3,-2)、A2(-1,3)、B2(-3,2).
已知:如图,△OAB,分别画出与△OAB关于x轴、y轴对称的图形△OA1B1和△OA2B2,△OA1B1和△OA2B2各顶点的坐标为O(0,0)、A1(1,-3)、B1(3,-2)、A2(-1,3)、B2(-3,2).