题目内容
5.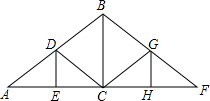 如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=12m,∠A=30°,则DE等于3.
如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=12m,∠A=30°,则DE等于3.
分析 由于BC、DE垂直于横梁AC,可得BC∥DE,而D是AB中点,可知AB=BD,利用平行线分线段成比例定理可得AE:CE=AD:BD,从而有AE=CE,即可证DE是△ABC的中位线,可得DE=$\frac{1}{2}$BC,在Rt△ABC中易求BC,进而可求DE.
解答 解:∵立柱BC、DE垂直于横梁AC,
∴BC∥DE,
∵D是AB中点,
∴AD=BD,
∴AE:CE=AD:BD,
∴AE=CE,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC,
在Rt△ABC中,BC=$\frac{1}{2}$AB=6,
∴DE=3.
故答案是:3.
点评 本题考查了平行线分线段成比例定理、三角形中位线定理、直角三角形30°的角所对的边等于斜边的一半.解题的关键是证明DE是△ABC的中位线.

练习册系列答案
相关题目
17.正六边形的一个外角的度数为( )
| A. | 36° | B. | 45° | C. | 60° | D. | 72° |
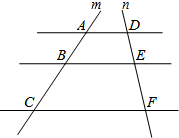 如图,直线AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=2,AC=5,DE=1.4,则DF的长为( )
如图,直线AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=2,AC=5,DE=1.4,则DF的长为( )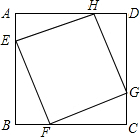 已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S.
已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S. 图(1)是一个小正方形体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是梦.
图(1)是一个小正方形体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是梦.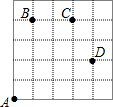 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4).其中第一数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4).其中第一数表示左右方向,第二个数表示上下方向,那么图中