题目内容
15.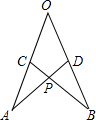 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )
如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )①△AOD≌△BOC;②△APC≌△BPD;③PC=PD.
| A. | ①②③ | B. | ①② | C. | ② | D. | ① |
分析 ①根据题中条件,由两边夹一角可得△AOD≌△BOC;
②根据全等三角形的性质得出对应角相等,又由已知得出AC=BD,可得△APC≌△BPD;
③根据等边三角形的性质和等量代换即可得到PC=PD.
解答 解:①在△AOD与△BOC中,
$\left\{\begin{array}{l}{OA=OB}\\{∠O=∠O}\\{OD=OC}\end{array}\right.$,
∴△AOD≌△BOC,故①正确;
②∵△AOD≌△BOC,
∴∠A=∠B,
又∵∠APC=∠BPD,
∴∠ACP=∠BDP,
OA-OC=OB-OD,即AC=BD,
在△APC与△BPD中,
$\left\{\begin{array}{l}{∠APC=∠BPD}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$,
∴△APC≌△BPD,故②正确;
③∵△AOD≌△BOC,
∴AD=BC,
∵△APC≌△BPD,
∴AP=BP,
∴AD-AP=BC-BP,
∴PC=PD,故③正确.
故选:A.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.

练习册系列答案
相关题目
6.某商场将进货单价为18元的商品,按每件20元售出时,每天可销售100件,如果每件提高1元,日销售量就要减少10件,若使商场投资少,收益大,那么该商品的售出价格定为多少元时,才能使每天获得350元?
10.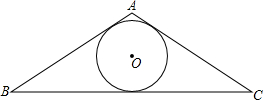 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )| A. | 点O在△ABC的三边垂直平分线上 | |
| B. | 点O在△ABC的三个内角平分线上 | |
| C. | 如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=$\frac{2S}{a+b+c}$ | |
| D. | 如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2 |
4.10月份某地四个楼盘的销售面积和销售单价如下表:
则这四个楼盘10月份销售均价为0.85万元/米2.
| 楼盘 | A | B | C | D |
| 销售面积(m2) | 10000 | 15000 | 10000 | 5000 |
| 销售单价(万元/m2) | 0.6 | 0.8 | 1 | 1.2 |
 如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=$\frac{4}{5}$,求sinC的值.
如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=$\frac{4}{5}$,求sinC的值. 如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.
如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.