题目内容
20.探究函数y=x+$\frac{9}{x}$的图象与性质(1)函数y=x+$\frac{9}{x}$的自变量x的取值范围是x≠0;
(2)下列四个函数图象中,函数y=x+$\frac{9}{x}$的图象大致是C;
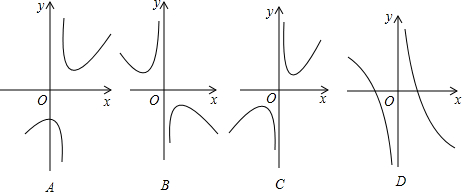
(3)对于函数y=x+$\frac{9}{x}$,求当x>0时,y的取值范围.
请将下面求解此问题的过程补充完整:
解:∵x>0,
∴y=x+$\frac{9}{x}$=($\sqrt{x}$)2+($\frac{3}{\sqrt{x}}$)2=($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2+6.
∵($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2≥0,
∴y≥6
(4)若函数y=$\frac{{{x^2}-4x+9}}{x}$,则y的取值范围是y≤-10或y≧2.
分析 (1)由分母不为0可得;
(2)由x≠0排除A,由y=$\frac{{x}^{2}+9}{x}$且x2+9>0知当x<0时y<0;当x>0时y>0可得答案;
(3)利用二次函数的配方法求解可得;
(4)分x>0和x<0仿照(3)中方法求解可得.
解答 解:(1)函数y=x+$\frac{9}{x}$的自变量x的取值范围是x≠0,
故答案为:x≠0.
(2)∵x≠0,
∴函数图象与y轴无交点,A选项排除;
∵y=$\frac{{x}^{2}+9}{x}$,且x2+9>0,
∴当x<0时,y<0;当x>0时,y>0;
∴符合题意得函数图象为C选项;
故选:C.
(3)∵x>0,
∴y=x+$\frac{9}{x}$=($\sqrt{x}$)2+($\frac{3}{\sqrt{x}}$)2=($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2+6.
∵($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2≥0,
∴y≥6,
故答案为:6,≥6;
(4)$y=\frac{{{x^2}-4x+9}}{x}$=$x+\frac{9}{x}-4$,
当x>0时,∵$x+\frac{9}{x}≥6$,
∴y≧2
当x<0时,-x>0,-$\frac{9}{x}>0$,-x-$\frac{9}{x}$=${(\sqrt{-x})^2}+{(\sqrt{-\frac{9}{x}})^2}$,
由(3)得,-x-$\frac{9}{x}$≧6,
所以$x+\frac{9}{x}≤-6$,
所以y≤-10,
y的取值范围是y≤-10或y≧2,
故答案为:y≤-10或y≧2.
点评 本题主要考查反比例函数的图象和性质,会用描点法画出函数图象,利用数形结合的思想写出函数的性质及二次函数的最值求法是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
| A地 | B地 | ||
| 每千顶帐篷 所需车辆数(单位:辆) | 甲市 | 4 | 7 |
| 乙市 | 3 | 5 | |
| 急需帐篷数(单位:千顶) | 9 | 11 | |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
| A. | 都是普查 | B. | 都是抽查 | C. | ①是普查②是抽查 | D. | ①是抽查②是普查 |
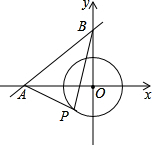 如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.
如图,直线y=$\frac{3}{4}$+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为11cm2.