题目内容
19.先化简,再求值:$(\frac{a-1}{{{a^2}-4a+4}}-\frac{a+2}{{{a^2}-2a}})÷(\frac{4}{a}-1)$,其中a是一元二次方程x2-4x-3=0的根.分析 先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 解:原式=[$\frac{a-1}{(a-2)^{2}}$-$\frac{a+2}{a(a-2)}$]÷$\frac{4-a}{a}$
=$\frac{a(a-1)-(a+2)(a-2)}{a(a-2)^{2}}$÷$\frac{4-a}{a}$
=$\frac{4-a}{a{(a-2)}^{2}}$•$\frac{a}{4-a}$
=$\frac{1}{{(a-2)}^{2}}$,
∵a是一元二次方程x2-4x-3=0的根,
∴a2-4a-3=0,解得a=2±$\sqrt{7}$,
当a=2+$\sqrt{7}$时,原式=$\frac{1}{{(2+\sqrt{7}-2)}^{2}}$=$\frac{1}{7}$;
当a=2-$\sqrt{7}$时,原式=$\frac{1}{{(2-\sqrt{7}-2)}^{2}}$=$\frac{1}{7}$.
故分式的值为$\frac{1}{7}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
14.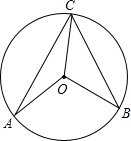 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
 读句画图:如图,A,B,C,D在同一平面内,
读句画图:如图,A,B,C,D在同一平面内,