题目内容
2.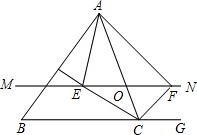 如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)
分析 (1)由平行线的性质和角平分线的定义得出∠OCE=∠OEC,∠OCF=∠OFC,得出EO=CO,FO=CO,即可得出结论;
(2)先证明四边形AECF是平行四边形,再由对角线相等,即可得出结论;
(3)由(2)得出四边形AECF是矩形,再由平行线得出AC⊥EF,得出四边形AECF是菱形,即可得出结论.
解答 解:(1)猜想:OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO.
(2)当点O运动到AC的中点时,四边形AECF是矩形;理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,
即AC=EF,
∴四边形AECF是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形;理由如下:
∵由(2)得:当点O运动到AC的中点时,四边形AECF是矩形,
∵MN∥BC,当∠ACB=90°时,
∴∠AOE=∠ACB=90°,
∴AC⊥EF,
∴四边形AECF是菱形,
∴四边形AECF是正方形.
点评 本题考查了平行线的性质、等腰三角形的判定、矩形的判定、菱形的判定、正方形的判定;熟练掌握平行线的性质和矩形、菱形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
12.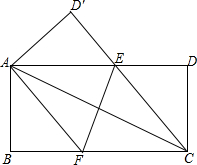 如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
(1)求EC的长度;
(2)证明:四边形AFCE是菱形.
 如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处(1)求EC的长度;
(2)证明:四边形AFCE是菱形.
10.下表是明明商行某商品的销售情况,该商品原价为560元,随着不同幅度的降价.
(1)每降价5元,日销量增加多少件?请你估计降价之前的日销量是多少?
(2)写出降价x(元)与日销量y(件)之间的关系式.
| 降价(单位:元) | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| 日销量(单位:件) | 780 | 810 | 840 | 870 | 900 | 930 | 960 |
(2)写出降价x(元)与日销量y(件)之间的关系式.
 如图,分别以△ABC的边AB、AC为直角边向外作等腰Rt△ABD、Rt△ACE.连结BE、CD,且交于点Q,求证:OA平分∠DOE.
如图,分别以△ABC的边AB、AC为直角边向外作等腰Rt△ABD、Rt△ACE.连结BE、CD,且交于点Q,求证:OA平分∠DOE.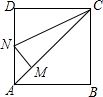 如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.
如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.