Question

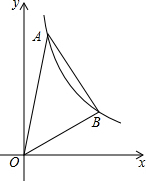如图，点A，B在反比例函数y=

2

x

（x＞0）的图象上，△OAB是以OA为斜边的等腰直角三角形，则△OAB的面积为

 

．

Answer 1

考点：全等三角形的判定与性质,反比例函数图象上点的坐标特征

专题：

分析：过B作x轴的垂线，垂足为C，过A作y轴的垂线，垂足为D，直线AD交BC于E，设B（a，b），先证明△ABE≌△BOC，得出BE=CO=a，AE=BC=b，根据点A、D是反比例函数上的点，得出有关三角形的面积，通过解方程组求出b²=-1+

5

，a²=1+

5

，即可得出结果．

解答： 解：过B作x轴的垂线，垂足为C，过A作y轴的垂线，垂足为D，直线AD交BC于E，如图所示：
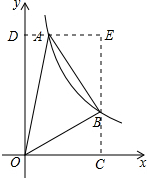设B（a，b），
∵△OAB是等腰直角三角形，
∴AB=OB，∠ABO=90°，
∴∠1+∠2=90°，
∵∠1+∠3=90°，
∴∠2=∠3，
在△ABE和△BOC中，

∠2=∠3   ∠BCO=∠AEB=90°   AB=BC

，
∴△ABE≌△BOC（AAS），
∴BE=CO=a，AE=BC=b，
∴AD=a-b，OD=a+b，
∴A（a-b，a+b），
∵S_△OAD=

1

2

（a+b）（a-b）=

1

2

×2=1，S_△OBC=

1

2

ab=1，
∴

a2-b2=2 ab=2

，
解得b²=-1+

5

，a²=1+

5

，
∴S_△OAB=S_矩形OCED-S_OBC-S_△OAD-S_△ABE
=a（a+b）-1-1-1
=a²+ab-3
=1+

5

+2-3
=

5

．
故答案为：

5

．

点评：本题考查了全等三角形的判定与性质以及反比例函数图象上点的坐标特征；通过作辅助线构造全等三角形，得出坐标之间的关系，通过解方程组求出答案是解题的关键．