题目内容
17. 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
分析 (1)由平行四边形的判定定理:两组对边分别平行得到结论;
(2)由角平分线、等量代换得到角相等,由等角对等边得到BD=AB=5,根据勾股定理列方程求解.
解答 (1)证明:∵∠ADE=∠BAD,
∴AB∥DE,
∵AE⊥AC,BD⊥AC,
AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:∵DA平分∠BDE,
∴∠AED=∠BDA,
∴∠BAD=∠BDA,
∴BD=AB=5,
设BF=x,则DF=5-x,
∴AD2-DF2=AB2-BF2,
∴62-(5-x)2=52-x2,
∴x=$\frac{7}{5}$,
∴AF=$\sqrt{{AB}^{2}{-BF}^{2}}$=$\frac{24}{5}$,
∴AC=2AF=$\frac{48}{5}$.
点评 本题考查了平行四边形的判定和性质,角平分线的性质,勾股定理的应用,解题的关键是利用勾股定理列方程.

练习册系列答案
相关题目
7.两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
| A. | 8和12 | B. | 9和11 | C. | 7和13 | D. | 6和14 |
8.把一枚均匀的骰子连续抛掷两次,则两次朝上面的点数之积为3的倍数的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{15}{36}$ | C. | $\frac{4}{11}$ | D. | $\frac{5}{9}$ |
6.$\sqrt{16}$的算术平方根是( )
| A. | 4 | B. | -4 | C. | 2 | D. | ±2 |
 如图,⊙O1的半径为1,⊙O2的半径为2,O1O2=5,⊙O分别与⊙O1外切、与⊙O2内切,那么⊙O半径r的取值范围是r≥3.
如图,⊙O1的半径为1,⊙O2的半径为2,O1O2=5,⊙O分别与⊙O1外切、与⊙O2内切,那么⊙O半径r的取值范围是r≥3.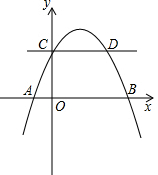 如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D.
如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D.