题目内容
8．把一枚均匀的骰子连续抛掷两次，则两次朝上面的点数之积为3的倍数的概率是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{15}{36}$ | C． | $\frac{4}{11}$ | D． | $\frac{5}{9}$ |
分析 根据题意，同时抛掷两个骰子，共6×6=36种情况，而向上的点数之积为3的倍数必须至少有一个骰子向上的点数为3的倍数，即3或6，然后利用概率公式求解即可．
解答 解：根据题意，同时抛掷两个骰子，共6×6=36种情况，
而向上的点数之积为3的倍数必须至少有一个骰子向上的点数为3的倍数，即3或6，
其情况数目为4×2+6×2=20种，
则向上的点数之积为3的倍数的概率$\frac{20}{36}$=$\frac{5}{9}$，
故选D．
点评 本题考查等可能事件的概率，本题的易错点在于计算向上的点数之积为3的倍数的情况数目，也可采用列表或列树状图的方法求解．
练习册系列答案
阅读快车系列答案
相关题目
18．在Rt△ABC中，∠C=90°，AB=4，D为斜边AB上的一个动点，作DE⊥AC于E，DF⊥BC于F，以EF为直径作一个圆，记圆的周长为l，则下面结论中错误的是（ ）
| A． | 若∠A=30°，则l的最小值等于$\sqrt{3}$π | B． | 若∠A=45°，则l的最小值等于2π | ||
| C． | 若∠A=60°，则l的最小值等于$\frac{\sqrt{3}}{2}$π | D． | 若EF∥AB，则l等于2π |
19．
如图，在△ABC中，D是BC上延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（ ）
如图，在△ABC中，D是BC上延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（ ）| A． | 20° | B． | 30° | C． | 70° | D． | 80° |
16．绝对值为2的实数是（ ）
| A． | 2 | B． | 2 | C． | -2 | D． | ±2 |
3．二次根式$\sqrt{（x+3）^{2}}$中字母x的取值范围是（ ）
| A． | x≠-3 | B． | x≥-3 | C． | x＞-3 | D． | 全体实数 |
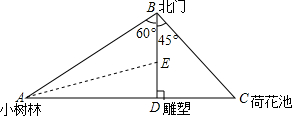某公园有一座雕塑D，在北门B的正南方向，BD为100米，小树林A在北门的南偏西60°方向，荷花池C在北门B的东南方向，已知A，D，C三点在同一条直线上且BD⊥AC：
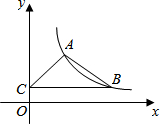在平面直角坐标系中，反比例函数y=$\frac{k}{x}$（x＞0，k＞0）的图象经过点A（m，n），B（2，1），且n＞1，过点B作y轴的垂线，垂足为C，若△ABC的面积为2，求点A的坐标．
如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC