题目内容
12. 如图,⊙O1的半径为1,⊙O2的半径为2,O1O2=5,⊙O分别与⊙O1外切、与⊙O2内切,那么⊙O半径r的取值范围是r≥3.
如图,⊙O1的半径为1,⊙O2的半径为2,O1O2=5,⊙O分别与⊙O1外切、与⊙O2内切,那么⊙O半径r的取值范围是r≥3.
分析 根据内切圆的圆心距等于半径之差,外切圆的圆心距等于半径之和,可得OO1,OO2,分类讨论:三圆心在同一条直线上,根据线段的和差,可得答案;三圆心不在同一条直线上,根据三角形三边的关系,可得答案.
解答 解:如图1:
2r=5+2-1=6,
解得r=3;
如图2:
由两边之和大于第三边,得
(r+1)+(r-2)>5,
解得r>3,
综上所述:r≥3.
故答案为:r≥3.
点评 本题考查了圆与圆的位置关系,利用了相切的关系:内切圆的圆心距等于半径之差,外切圆的圆心距等于半径之和,分类讨论是解题关键.

练习册系列答案
相关题目
3.二次根式$\sqrt{(x+3)^{2}}$中字母x的取值范围是( )
| A. | x≠-3 | B. | x≥-3 | C. | x>-3 | D. | 全体实数 |
20.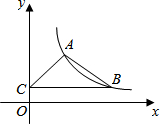 在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
 在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
4.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{64}$=4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{25\frac{1}{9}}$=5$\frac{1}{3}$ |
 尺规作图,已知半圆如图,请以直径为底,半径为腰上的高作等腰三角形(不写作法,保留痕迹).
尺规作图,已知半圆如图,请以直径为底,半径为腰上的高作等腰三角形(不写作法,保留痕迹). 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC