题目内容
3.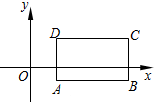 如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).
如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).(1)写出顶点B和D的坐标;
(2)若点M为第四象限内一点,且使△MAB与△CAB全等,写出点M的坐标;
(3)若△MAB中任意一点P(x0,y0)经平移后对应点为P1(x0-6,y0-2),将△MAB作同样的平移得到△M1A1B1.写出M1的坐标.
分析 (1)根据长方形的性质可得顶点的坐标特点,得出坐标;
(2)根据△MAB与△CAB全等,且点M为第四象限内一点可得的M的坐标;
(3)根据平移的特点进行解答即可.
解答 解:(1)因为长方形ABCD的两个的坐标为A(2,-1),C(8,3),
可得:B(8,-1),D(2,3);
(2)因为点M为第四象限内一点,且△MAB与△CAB全等,
可得:BM=BC,AM=AD,
所以点M的坐标为(8,-5)或(2,-5);
(3)因为△MAB中任意一点P(x0,y0)经平移后对应点为P1(x0-6,y0-2),将△MAB作同样的平移得到△M1A1B1,
所以点M1的坐标为(-4,-7)或(2,-7).
点评 此题考查全等三角形的判定和性质,关键是长方形的性质和全等三角形的性质得出点的坐标.

练习册系列答案
相关题目
18.在平面直角坐标系中,若点P关于x轴的对称点在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
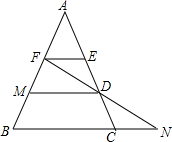 已知,如图在△ABC中,AE=ED=DC,FE∥MD∥BC,FD的延长线交BC的延长线于N,则$\frac{EF}{BN}$为$\frac{1}{4}$.
已知,如图在△ABC中,AE=ED=DC,FE∥MD∥BC,FD的延长线交BC的延长线于N,则$\frac{EF}{BN}$为$\frac{1}{4}$.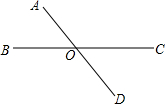 如图,直线AD、BC交于点O,且∠AOB+∠COD=100°,则∠AOC的度数为125°.
如图,直线AD、BC交于点O,且∠AOB+∠COD=100°,则∠AOC的度数为125°.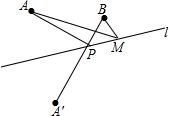 如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.
如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.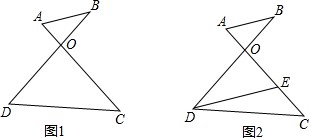 如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.
如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.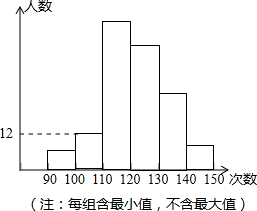 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题: 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒: