题目内容
11.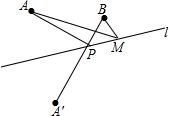 如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.
如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.(1)求AP+PB.
(2)若点M是直线l上异于点P的任意一点,求证:AM+MB>AP+PB.
分析 (1)由轴对称的性质可知:PA=PA′,从而可求得答案;
(2)由两点之间线段最短进行证明即可.
解答 解:(1)∵点A′与A关于直线l对称,
∴PA=PA′.
∴PA+PB=PA′+PB=A′B=a.
(2)∵点A′与A关于直线l对称,
∴MA=MA′.
∴AM+BM=MA′+MB.
由(1)可知:AP+PB=A′B
由两点之间线段最短可知:MA′+MB>A′B,即AM+MB>AP+PB.
点评 本题主要考查的是轴对称的性质和线段的性质,掌握轴对称的性质是解题的关键.

练习册系列答案
相关题目
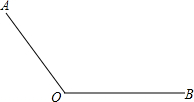 如图,已知∠AOB.
如图,已知∠AOB.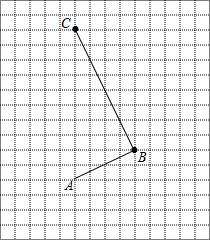 如图,网格中每一个小正方形的边长为1个单位长度.
如图,网格中每一个小正方形的边长为1个单位长度.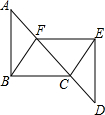 如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)
如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)
 如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.
如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.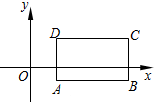 如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).
如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).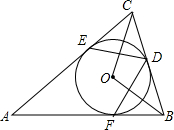 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.