题目内容
3.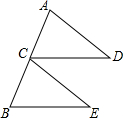 如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
分析 根据SAS证明△ACD≌△CBE,再利用全等三角形的性质解答即可.
解答 解:∵C是AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,∠DCE=∠E,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACD=∠CBE}\\{CD=BE}\end{array}\right.$,
∴△ACD≌△CBE(SAS),
∴AD=CE,∠D=∠E,
∴∠DCE=∠D,
∴AD∥CE,
所以AD与CE平行且相等.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ACD≌△CBE.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
13.抛物线y=-x2-2x+1的对称轴为( )
| A. | x=-1 | B. | x=1 | C. | x=-2 | D. | x=2 |
14.已知代数式x+2y的值是-3,则代数式2x+4y+1的值是( )
| A. | -6 | B. | -5 | C. | -4 | D. | -3 |
18.若关于x的方程$\frac{3x+a}{x-1}$=1的解是正数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1且a≠0 | C. | a<-1 | D. | a<-1且a≠-3 |
 将连续的整数1,2,3,4,…排列成如下的数表,用3×3正方形框框出9个数(如图).
将连续的整数1,2,3,4,…排列成如下的数表,用3×3正方形框框出9个数(如图).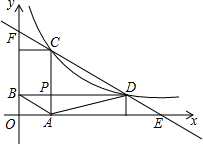 如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.
如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.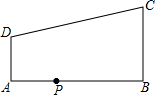 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )