题目内容
16.某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A种产品需这种原料2吨,生产费用1000元;每生产1吨B种产品需这种原料2.5吨,生产费用900元.如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?分析 设A产品生产x吨,B产品生产y吨,根据生产A、B两种产品需要的原料是1200吨和费用为530000元建立方程组求出其解即可.
解答 解:设A产品生产x吨,B产品生产y吨,由题意,得
$\left\{\begin{array}{l}{2x+2.5y=1200}\\{1000x+900y=530000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=350}\\{y=200}\end{array}\right.$.
答:A产品生产350吨,B产品生产200吨.
点评 本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,找出题目蕴含的数量关系是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
6.根据表格的对应值得到函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象与x轴有一个交点的横坐标x的范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| y=ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
| A. | x<3.23 | B. | 3.23<x<3.24 | C. | 3.24<x<3.25 | D. | 3.25<x<3.26 |
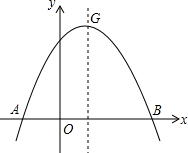 如图,抛物线y=-x2+tx+2t2(t>0)与x轴交于A、B两点,点A在点B的左边,抛物线顶点为G.
如图,抛物线y=-x2+tx+2t2(t>0)与x轴交于A、B两点,点A在点B的左边,抛物线顶点为G.