题目内容
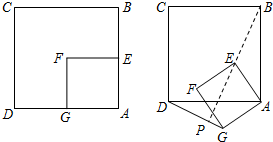 如图,正方形ABCD和正方形AEFG,边AE在边AB上,AB=2AE=2.将正方形AEFG绕点A逆时针旋转60°,BE的延长线交直线
如图,正方形ABCD和正方形AEFG,边AE在边AB上,AB=2AE=2.将正方形AEFG绕点A逆时针旋转60°,BE的延长线交直线DG于点P,旋转过程中点P运动的路线长为
考点:旋转的性质,正方形的性质,弧长的计算
专题:
分析:根据全等三角形对应角相等可得∠ADG=∠ABE,然后求出∠BPD=∠BAD=90°,易知△OFA是等边三角形,∠AOF=60°,然后根据弧长公式列式计算即可得解.
解答: 解:在△DAG和△BAE中
解:在△DAG和△BAE中
,
∴△DAG≌△BAE(SAS),
∴∠ADG=∠ABE,
如图1,∵∠1=∠2,
∴∠BPD=∠BAD=90°,
连接BD,则△BPD是以BD为斜边的直角三角形,
设BD的中点为O,连接OP,则OP=
BD=
AB=
,
∴旋转过程中,点P运动的路线是以O为圆心,以OP为半径的一段弧,
如图2,当边AE在边AB上时,P与A重合,当∠BAE=60°时,设AB的中点为M,连接ME,则AE=AM=BM=
AB,
∴△AEM是等边三角形,
∴∠EMA=60°,∠MBE=∠MEB=30°,
∴∠BEA=90°,
∴B、E、F三点共线,
∴P与F重合,
连接AF,可得△OFA是等边三角形,∠AOF=60°,
∴点P运动的路线长为:
×
=
π.
故答案为:
π.
 解:在△DAG和△BAE中
解:在△DAG和△BAE中
|
∴△DAG≌△BAE(SAS),
∴∠ADG=∠ABE,
如图1,∵∠1=∠2,
∴∠BPD=∠BAD=90°,
连接BD,则△BPD是以BD为斜边的直角三角形,
设BD的中点为O,连接OP,则OP=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴旋转过程中,点P运动的路线是以O为圆心,以OP为半径的一段弧,
如图2,当边AE在边AB上时,P与A重合,当∠BAE=60°时,设AB的中点为M,连接ME,则AE=AM=BM=
| 1 |
| 2 |
∴△AEM是等边三角形,
∴∠EMA=60°,∠MBE=∠MEB=30°,
∴∠BEA=90°,
∴B、E、F三点共线,
∴P与F重合,
连接AF,可得△OFA是等边三角形,∠AOF=60°,
∴点P运动的路线长为:
| 2 |
| 60π |
| 180 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:此题主要考查了旋转的性质和等边三角形的判定与性质以及弧长公式应用等知识,难点在于判断出路线是以BD为直径的弧长的一部分.

练习册系列答案
相关题目
 如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.
如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.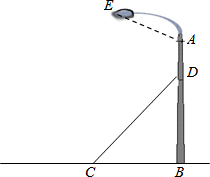 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且CB=5米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且CB=5米.