题目内容
14.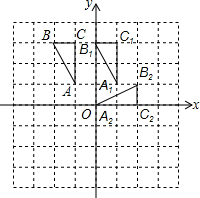 如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题:
如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题:(1)△ABC沿x轴正方向平移2个单位得到△A1B1C1,则B1的坐标是(0,2);
(2)△A1B1C1绕点(0,1)顺时针旋转90°得到△A2B2C2,则B2的坐标是(2,1);
(3)两次变换中线段AB所扫过的面积之和为(4+$\frac{3}{4}$π)平方单位.
分析 (1)利用平移的性质画出点A、B、C的对应点A1、B1、C1,然后写出B1点的坐标;
(2)利用网格特点和旋转的性质画出△A2B2C2,然后写出B2的坐标;
(3)计算平行四边形和圆环的面积即可.
解答  解:(1)点B1的坐标为((0,2);
解:(1)点B1的坐标为((0,2);
(2)点B2的坐标为(2,1);
(3)两次变换中线段AB所扫过的面积之和=2×2+$\frac{90π•({2}^{2}-{1}^{2})}{360}$=4+$\frac{3}{4}$π.
故答案为(0,2),(2,1),4+$\frac{3}{4}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
4.已知点(m-1,n+2)与(2m-4,2)关于x轴对称,则(m+n)2015的值是( )
| A. | 1 | B. | -1 | C. | 2013 | D. | -2013 |
4.在下列式子中,是一元一次方程的是( )
| A. | 2x+1 | B. | 2x+1=3 | C. | 7x+5y=0 | D. | x2-x=0 |
 如图,直线y=x+3与y=kx交于(1,m),根据图象试求m和k的值.
如图,直线y=x+3与y=kx交于(1,m),根据图象试求m和k的值.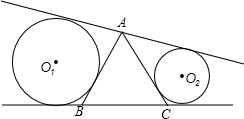 如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数. 如图,在△ABC中.∠A=30°,AC=8,BC=5.以直线AB为轴,将△ABC旋转一周得到一个旋转体,求这个旋转体的全面积.
如图,在△ABC中.∠A=30°,AC=8,BC=5.以直线AB为轴,将△ABC旋转一周得到一个旋转体,求这个旋转体的全面积.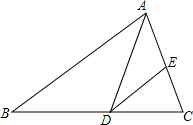 如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由.
如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由. 如图,有两条长为10cm的纸带重叠摆放在一起(重叠部分为B).若A,B,C三部分的面积之比为3:2:3.则重叠部分B纸带的长度为4cm.
如图,有两条长为10cm的纸带重叠摆放在一起(重叠部分为B).若A,B,C三部分的面积之比为3:2:3.则重叠部分B纸带的长度为4cm. 如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3.
如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3.