题目内容
12. △ABC中,∠ACB=90°,点D是AC上一点,CE⊥BD于E,∠DAE=∠ABD,求证:
△ABC中,∠ACB=90°,点D是AC上一点,CE⊥BD于E,∠DAE=∠ABD,求证:(1)△DAE∽△DBA:
(2)AD=CD.
分析 (1)根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到$\frac{AD}{DE}=\frac{BD}{AD}$,于是得到AD2=DE•BD,由△CDE∽△BCD,得到$\frac{CD}{BD}=\frac{DE}{CD}$,于是得到CD2=DE•BD,等量代换得到AD2=CD2,即可得到结论.
解答 证明:(1)∵∠DAE=∠ABD,∠ADE=∠BDA,
∴△DAE∽△DBA;
(2)∵△DAE∽△DBA,
∴$\frac{AD}{DE}=\frac{BD}{AD}$,
∴AD2=DE•BD,
∵CE⊥BD,
∴∠ACB=∠CDE=90°,
∵∠CDE=∠BDC,
∴△CDE∽△BCD,
∴$\frac{CD}{BD}=\frac{DE}{CD}$,
∴CD2=DE•BD,
∴AD2=CD2,
∴AD=CD.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4.在下列式子中,是一元一次方程的是( )
| A. | 2x+1 | B. | 2x+1=3 | C. | 7x+5y=0 | D. | x2-x=0 |
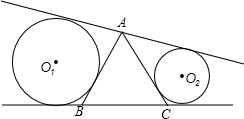 如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数. 如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3.
如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3. 如图所示一块长为20cm,宽10cm的矩形方框,镶在其外围的木质边框宽2cm,边框的内外边缘所成的矩形相似吗?为什么?
如图所示一块长为20cm,宽10cm的矩形方框,镶在其外围的木质边框宽2cm,边框的内外边缘所成的矩形相似吗?为什么? 如图,共有5个角,分别是∠AOD,∠AOC,∠DOC,∠DOB,∠COB.
如图,共有5个角,分别是∠AOD,∠AOC,∠DOC,∠DOB,∠COB.