题目内容
 如图,?ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AB=BF,②AF=CF+CD,③AF=CF+AD,④AE⊥EF,其中正确的是( )
如图,?ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AB=BF,②AF=CF+CD,③AF=CF+AD,④AE⊥EF,其中正确的是( )| A、①② | B、②④ | C、③④ | D、①②④ |
考点:平行四边形的性质,全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:首先延长AD,交FE的延长线于点M,易证得△DEM≌△CEF,即可得EM=EF,又由AE平分∠FAD,即可判定△AEM是等腰三角形,由三线合一的知识,可得AE⊥EF.
解答: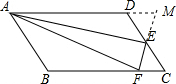 解:延长AD,交FE的延长线于点M,
解:延长AD,交FE的延长线于点M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
,
∴△DEM≌△CEF(AAS),
∴EM=EF,
∵AE平分∠FAD,
∴AM=AF,AE⊥EF.
即AF=AD+DM=CF+AD;故③,④正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故①错误.
故选C.
 解:延长AD,交FE的延长线于点M,
解:延长AD,交FE的延长线于点M,∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
|
∴△DEM≌△CEF(AAS),
∴EM=EF,
∵AE平分∠FAD,
∴AM=AF,AE⊥EF.
即AF=AD+DM=CF+AD;故③,④正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故①错误.
故选C.
点评:此题考查了平行四边形的性质、等腰三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知线段AB=10,点P是线段AB的黄金分割点,那么线段PB的长约为( )
如图,已知线段AB=10,点P是线段AB的黄金分割点,那么线段PB的长约为( )| A、6.18 | B、0.382 |
| C、0.618 | D、3.82 |
 如图是第二届全运会的吉祥物宁宁,下列图案是由宁宁通过平移得到的是( )
如图是第二届全运会的吉祥物宁宁,下列图案是由宁宁通过平移得到的是( )A、 |
B、 |
C、 |
D、 |
如果∠α与∠β互余,∠α=40°,那么∠β的补角的度数是( )
| A、30° | B、45° |
| C、90° | D、130° |
某班同学毕业时将自己的照片向全班其他同学各送一张表示留念,全班共送2450张照片,如果全班有x名同学,根据题意,列出方程为( )
| A、x(x+1)=2450 |
| B、x(x-1)=2450×2 |
| C、x(x-1)=2450 |
| D、2x(x+1)=2450 |