题目内容
若?ABCD中一内角平分线和某边相交把这条边分成1cm、2cm的两条线段,则?ABCD的周长是 cm.
考点:平行四边形的性质
专题:
分析:根据题意画出图形,由平行四边形得出对边平行,又由角平分线可以得出△ABE为等腰三角形,可以求解.
解答: 解:∵四边形ABCD为平行四边形,
解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE为角平分线,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴AB=BE.
①当BE=1cm时,CE=2cm,AB=1cm,则周长为2×(1+2+1)=8cm;
②当BE=2cm时,CE=1cm,AB=2cm,则周长为2×(2+1+2)=10cm.
综上所述,?ABCD的周长是8或10cm.
故答案是:8或10.
 解:∵四边形ABCD为平行四边形,
解:∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠DAE=∠AEB,
∵AE为角平分线,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴AB=BE.
①当BE=1cm时,CE=2cm,AB=1cm,则周长为2×(1+2+1)=8cm;
②当BE=2cm时,CE=1cm,AB=2cm,则周长为2×(2+1+2)=10cm.
综上所述,?ABCD的周长是8或10cm.
故答案是:8或10.
点评:本题考查了平行四边形的性质,结合了等腰三角形的判定.注意有两种情况,要进行分类讨论.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
不等式-2x<4的解集是( )
A、 |
B、 |
C、 |
D、 |
 如图,△ABC中,已知BC=12,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为28,则AC的长为
如图,△ABC中,已知BC=12,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为28,则AC的长为 如图,矩形零件上两孔中心A、B的距离是
如图,矩形零件上两孔中心A、B的距离是 如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N,若AB=13,AD=14,CM=9,则直径AC的长度为
如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N,若AB=13,AD=14,CM=9,则直径AC的长度为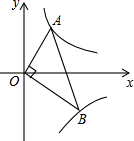 已知点A、B分别在反比例函数
已知点A、B分别在反比例函数 如图,?ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AB=BF,②AF=CF+CD,③AF=CF+AD,④AE⊥EF,其中正确的是( )
如图,?ABCD中,AB≠BC,F是BC上一点,AE平分∠FAD,且E是CD的中点,则下列结论:①AB=BF,②AF=CF+CD,③AF=CF+AD,④AE⊥EF,其中正确的是( )