题目内容
13.如图,△ABC中,AC=AB,以AB为直径作半圆O,交AC于点E,交BC于点D.(1)如图1,求证:CD=BD;
(2)如图2,连接CO交半圆O于点F,若AB=10,AE=8,求CF的长.
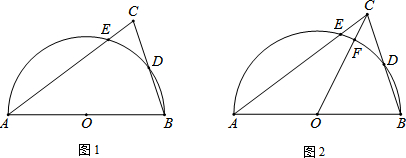
分析 (1)连接AD,根据直径所对的圆周角是直角和等腰三角形三线合一,证明CD=BD;
(2)根据切割线定理列出关于CF的方程,解方程得到答案.
解答 (1)证明:连接AD,
∵AB为直径,
∴∠ADB=90°,
∵AB=AC,
∴CD=BD;
(2)解:延长CD交⊙O于点F,
根据切割线定理,
CE•CA=CF•CH,
2×10=CF•(CF+10)
解得:CF=3$\sqrt{5}$-5,CF=-3$\sqrt{5}$-5(舍去)
点评 本题考查的是圆周角定理和切割线定理,解题的关键是正确作出辅助线,然后运用相应的定理进行解答,在解答时,要灵活运用所学的知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.某企业为了增收节支,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
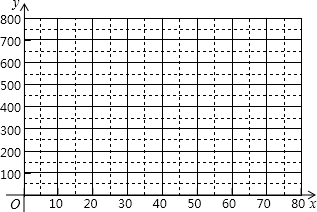
(1)把上表中x、y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想y与x之间的函数关系式,并求出函数关系式;
(2)市物价部门规定,销售部门规定该工艺品单价不得超过48元,要想每天获得8750元利润,单价应定为多少元?(利润=销售总价-成本总价 )
| 销售单价x元/件 | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y件 | … | 500 | 400 | 300 | 200 | 100 | … |

(1)把上表中x、y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想y与x之间的函数关系式,并求出函数关系式;
(2)市物价部门规定,销售部门规定该工艺品单价不得超过48元,要想每天获得8750元利润,单价应定为多少元?(利润=销售总价-成本总价 )
2.已知函数y=$\frac{k}{x}$的图象经过点(-1,2),则y=kx的图象( )
| A. | 在一、三象限 | B. | 在一、二象限 | C. | 在二、三象限 | D. | 在二、四象限 |
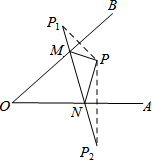 如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为( )
如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为( )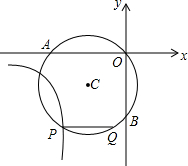 如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.
如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.
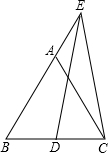 如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为2.
如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为2.