题目内容
 某舰艇以28海里/小时向东航行.在A处测得灯塔M在北偏东60°方向,半小时后到B处.又测得灯塔M在北偏东45°方向,此时灯塔与舰艇的距离MB是( )海里.
某舰艇以28海里/小时向东航行.在A处测得灯塔M在北偏东60°方向,半小时后到B处.又测得灯塔M在北偏东45°方向,此时灯塔与舰艇的距离MB是( )海里.A、7(
| ||||
B、14
| ||||
C、7(
| ||||
| D、14 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作MC⊥AB,垂足为C.设BC=CM=a,然后在Rt△ACM中,利用∠MAC的正切值,得到
=tan30°,从而得到
=
,然后求出a的长.
| MC |
| AC |
| a |
| a+14 |
| ||
| 3 |
解答: 解:作MC⊥AB,垂足为C.
解:作MC⊥AB,垂足为C.
∵∠MBC=45°,
∴∠BMC=45°,
设BC=CM=a,
在Rt△ACM中,
=tan30°,
则
=
,
解得,a=7
+7.
故选A.
 解:作MC⊥AB,垂足为C.
解:作MC⊥AB,垂足为C.∵∠MBC=45°,
∴∠BMC=45°,
设BC=CM=a,
在Rt△ACM中,
| MC |
| AC |
则
| a |
| a+14 |
| ||
| 3 |
解得,a=7
| 3 |
故选A.
点评:本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
△ABO的顶点坐标分别是A(-3,3)、B(3,3)、O(0,0),试将△ABO放大,使△ABO与△EFO的位似比为1:2,则点E和点F的坐标可能分别为( )
| A、(-6,6),(6,6) |
| B、(6,-6),(6,6) |
| C、(-6,6),(6,-6) |
| D、(6,6),(-6,-6) |
 如图所示,∠AOB和∠COD有公共顶点,AD⊥OC,BO⊥OD,∠AOB:∠COD=1:3,求∠AOB,∠COB的度数.
如图所示,∠AOB和∠COD有公共顶点,AD⊥OC,BO⊥OD,∠AOB:∠COD=1:3,求∠AOB,∠COB的度数.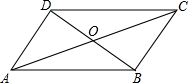 如图,在?ABCD中,对角线AC,BD相交于点O,AD=3
如图,在?ABCD中,对角线AC,BD相交于点O,AD=3 ?ABCD的边AB在x轴,顶点D在y轴上,点A的坐标为(-2,0),AD=4,AB=5.
?ABCD的边AB在x轴,顶点D在y轴上,点A的坐标为(-2,0),AD=4,AB=5. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是
如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是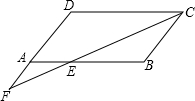 已知:如图,?ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F.
已知:如图,?ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F.