Question

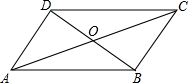如图，在?ABCD中，对角线AC，BD相交于点O，AD=3

3

，BD=6，AC=12，求?ABCD的面积．

Answer 1

考点：平行四边形的性质

专题：

分析：首先利用勾股定理的逆定理可证明△AOD是直角三角形，所以三角形ADB的面积可求，因为四边形ABCD是平行四边形，所以?ABCD的面积=2△ADB的面积，问题得解．

解答：解：∵四边形ABCD是平行四边形，
∴AO=CO=

1

2

AC=6，BO=DO=

1

2

BD=3，
∵AD=3

3

，
∴DO²+AD²=A0²=36，
∴△AOD是直角三角形，
∴三角形ADB的面积=

1

2

AD•BD=3

3

×6=18

3

，
∴?ABCD的面积=2△ADB的面积=36

3

．

点评：本题考查了平行四边形的性质、勾股定理的逆定理以及三角形的面积公式的运用，解题的关键是证明△AOD是直角三角形．