Question

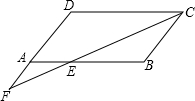已知：如图，?ABCD中，∠BCD的平分线交AB于E，交DA的延长线于F．
（1）求证：DF=DC；
（2）请你添加一个条件

 

，使得AE=BE．

Answer 1

考点：平行四边形的性质

专题：

分析：（1）由平行四边形的性质结合角平分线的定义可证得∠F=∠DCF，可证明DF=DC；
（2）要使AE=BE，则可知E为AB中点，则可知A为DF的中点，所以可添加A为DF中点．

解答：（1）证明：∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠F=∠BCF，
又∵CF平分∠BCD，
∴∠BCF=∠DCF，
∴∠F=∠DCF，
∴DF=DC；
（2）解：若AE=BE，则E为AB中点，
则可知AE=

1

2

CD，
∴AE为△FCD的中位线，
∴A为FD的中点，
∴可添加A为FD的中点，
故答案为：A为FD的中点．

点评：本题主要考查平行四边形的性质和判定，掌握平行四边形的性质和判定是解题的关键，即①两组对边分别平行的四边形?平行四边形，②两组对边分别相等的四边形?平行四边形，③一组对边分别平行且相等的四边形?平行四边形，④两组对角分别相等的四边形?平行四边形，⑤对角线互相平分的四边形?平行四边形．