题目内容
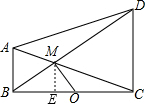
直角梯形ABCD中，AB∥CD，AB⊥BC，AC与BD交于M点，点O是BC中点，AB=2，CD=4，BC=6，则OM的长为考点：相似三角形的判定与性质,勾股定理
专题：压轴题
分析：过点M作ME⊥BC于E，可以得出AB∥ME∥CD，就可以得出
=
=
=
，△BME∽△BDC，由相似三角形的性质就可以求出BE、ME的值，由勾股定理就可以求出OM的值．
| AB |
| CD |
| AM |
| CM |
| BM |
| DM |
| 1 |
| 2 |
解答：解：过点M作ME⊥BC于E，
∴∠MEB=∠MEC=90°．
∵AB⊥BC，
∴∠ABC=90°．
∴∠ABC=∠MEC，
∴AB∥ME．
∵AB∥CD，
∴AB∥ME∥CD．
∴△ABM∽△CDM，△BME∽△BDC，
∴
=
=
.
=
．
∵AB=2，CD=4，
∴
=
=
=
，
∴
=
，
∴
=
，
∴
=
，
∴
=
，
即BE=2．
∵△BME∽△BDC，
∴
=
，
∴
=
，
∴ME=
．
∵点O是BC中点，
∴BO=
BC=3．
∴EO=BO-BE=3-2=1．
在Rt△MEO中，由勾股定理，得
MO=
=
．
故答案为：
．
∴∠MEB=∠MEC=90°．
∵AB⊥BC，
∴∠ABC=90°．
∴∠ABC=∠MEC，
∴AB∥ME．
∵AB∥CD，
∴AB∥ME∥CD．
∴△ABM∽△CDM，△BME∽△BDC，
∴
| AB |
| CD |
| AM |
| CM |
| BM |
| DM |
| MB |
| MD |
| BE |
| CE |
∵AB=2，CD=4，
∴
| AB |
| CD |
| AM |
| CM |
| BM |
| DM |
| 1 |
| 2 |
∴
| BE |
| CE |
| BM |
| MD |
∴
| BE |
| CE |
| 1 |
| 2 |
∴
| BE |
| BC |
| 1 |
| 3 |
∴
| BE |
| 6 |
| 1 |
| 3 |
即BE=2．
∵△BME∽△BDC，
∴
| ME |
| CD |
| BE |
| BC |
∴
| ME |
| 4 |
| 1 |
| 3 |
∴ME=
| 4 |
| 3 |
∵点O是BC中点，
∴BO=
| 1 |
| 2 |
∴EO=BO-BE=3-2=1．
在Rt△MEO中，由勾股定理，得
MO=
|
| 5 |
| 3 |
故答案为：
| 5 |
| 3 |
点评：本题考查了平行线的性质的运用，相似三角形的判定与性质的运用，勾股定理的运用，线段中点的定义的运用，解答时证明三角形相似是解答本题的关键．
练习册系列答案
相关题目
如图，某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB，在D处用高1.2米的测角仪CD，测得最高点A的仰角为32.6°，再向“太阳鸟”的方向前进20米至D′处，测得最高点A的仰角为45°，点D、D′、B在同一条直线上．求“太阳鸟”的高度AB．（精确到0.1米）下列调查中，适宜采用全面调查（普查）方式的是（ ）
| A、调查全国餐饮业用油合格率 |
| B、调查全国城镇居民居住的住房拥有情况 |
| C、调查某班学生1分钟跳绳的成绩 |
| D、调查我市中学生周末的娱乐方式 |
-
的倒数是（ ）
| 2 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、|-
|
如图，已知直线EF∥x轴，点E的坐标是（0，-4），又知抛物线y=ax2-2ax-3a与x轴交于A，B两点，与y轴交于点P（0，m）．计算8a3•（-2a）2的结果是（ ）
| A、32a5 |
| B、-32a5 |
| C、32a6 |
| D、-32a6 |
有5张正面分别标有数字-1，0，1，2，3的不透明卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后[从中任取一张，将该卡片上的数字记为m，则使关于x的二次函数y=x2-2mx+1的图象与端点为A（-1，1）和B（4，3）的线段（如图）只有一个交点的概率为