题目内容
 如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)
如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)[参考数据:sin32.6°=0.54,cos32.6°=0.84,tan32.6°=0.64].
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设AE=x,在Rt△ACE中表示出CE,在Rt△AC'E中表示出C'E,再由CC'=20米,可得出关于x的方程,解出即可得出答案.
解答:解:设AE=x,
在Rt△ACE中,CE=
=
x,
在Rt△AC'E中,C'E=
=x,
由题意得,CC'=CE-C'E=
x-x=20,
解得:x=
,
故AB=AE+BE=
+1.2≈36.8米.
答:“太阳鸟”的高度AB为36.8米.
在Rt△ACE中,CE=
| AE |
| tan32.6° |
| 25 |
| 16 |
在Rt△AC'E中,C'E=
| AE |
| cot45° |
由题意得,CC'=CE-C'E=
| 25 |
| 16 |
解得:x=
| 320 |
| 9 |
故AB=AE+BE=
| 320 |
| 9 |
答:“太阳鸟”的高度AB为36.8米.
点评:本题考查了解直角三角形的应用,解答本题要求学生能借助仰角构造直角三角形并解直角三角形,难度一般.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
把4a2-16因式分解的结果是( )
| A、4(a2-4) |
| B、(2a+4)(2a-4) |
| C、4(a-2)2 |
| D、4(a+2)(a-2) |
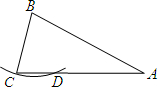 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )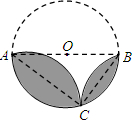 如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为
如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为 为了了解某校九年级学生在第一次模拟考试中的数学成绩(满分120分),随机抽查了部分学生的错解(均为整数),整理并制作图表(均不完整)如下:
为了了解某校九年级学生在第一次模拟考试中的数学成绩(满分120分),随机抽查了部分学生的错解(均为整数),整理并制作图表(均不完整)如下: 直角梯形ABCD中,AB∥CD,AB⊥BC,AC与BD交于M点,点O是BC中点,AB=2,CD=4,BC=6,则OM的长为
直角梯形ABCD中,AB∥CD,AB⊥BC,AC与BD交于M点,点O是BC中点,AB=2,CD=4,BC=6,则OM的长为