题目内容
16.如图(1),线段AB与射线OC相交于点O,且∠BOC=60°,AO=3,OB=1,动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,设运动时间为t秒.(1)当t=3秒时,则OP=3,S△APO:S△ABP=3:4;
(2)当△OPB是直角三角形时,求t的值;
(3)如图(2),当AP=AB,过点A作AQ∥BP,并使得∠QOP=∠B,连接QP,QO、AP交于点F,试证明△APQ∽△BPO.
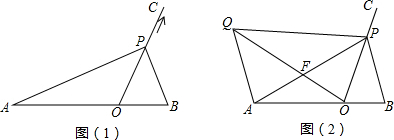
分析 (1)由动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,即可得当t=3秒时,则OP=3,又由△APO与△ABP等高,可得其面积比等于其对应底的比;
(2)由∠BOP=60°,可得当△OPB是直角三角形时,∠BOP=90°或∠BPO=90°,然后利用含30°的直角三角形的性质求解即可求得答案;
(3)由AQ∥BP,又由∠QOP=∠B,易证得△QFA∽△PFO,即可得$\frac{FQ}{FA}=\frac{FP}{FO}$,又由∠PFQ=∠OFA,证得△PFQ∽△OFA,继而证得结论.
解答 解:(1)∵动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,
∴t=3时,OP=3;
设P到AB的距离为h,则S△APO=$\frac{1}{2}$OA•h,S△ABP=$\frac{1}{2}$AB•h,
∵AO=3,OB=1,
∴AB=AO+OB=4,
∴S△APO:S△ABP=OA:AB=3:4;
故答案为:3,3:4;
(2)①∵∠BOP=60°,
∴∠BOP不为直角;
②当∠OBP=90°时,如图(a)所示,
∵∠BOP=60°,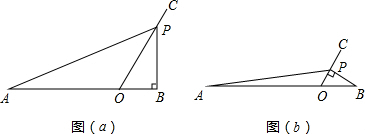
∴∠OPB=30°,
∴OP=2OB=2,
∴t=2s;
③当∠OPB=90°时,如图(b)所示,
∵∠BOP=60°,
∴∠OBP=30°,
∴OB=2OP,
∴2t=1,
∴t=$\frac{1}{2}$s,
综上,当△OPB为直角三角形时,t=2s或$\frac{1}{2}$s;
(3)∵AQ∥BP,
∴∠QAP=∠APB,
∵AP=AB,
∴∠APB=∠B,
∴∠QAP=∠B,
又∵∠QOP=∠B,
∴∠QAP=∠QOP,
又∵∠QFA=∠PFO,
∴△QFA∽△PFO,
∴$\frac{FQ}{FP}=\frac{FA}{FO}$,
即$\frac{FQ}{FA}=\frac{FP}{FO}$,
又∵∠PFQ=∠OFA,
∴△PFQ∽△OFA,
∴∠QPA=∠QOA.
∵∠AOC=∠OPB+∠B=∠QOA+∠QOP,∠B=∠QOP,
∴∠QOA=∠OPB,
∴∠OPB=∠QPA.
∴△APQ∽△BPO.
点评 此题属于相似三角形的综合题.考查了相似三角形的判定与性质、含30°的直角三角形的性质以及动点问题.注意掌握分类讨论思想的应用是解此题的关键.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 4,5,6 | B. | 1,1,2 | C. | 8,15,17 | D. | 5,12,23 |
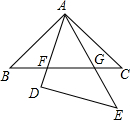 如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.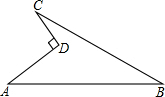 如图所示的一块地,其中∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,
如图所示的一块地,其中∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,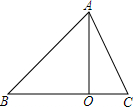 如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )
如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )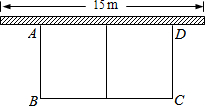 如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?
如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?


