题目内容
17.下列运算中错误的是( )| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$ | C. | $\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{{{(\sqrt{2}-\sqrt{3})}^2}}=\sqrt{2}-\sqrt{3}$ |
分析 利用二次根式的乘法法则对A进行判断;根据二次根式的加减法对B进行判断;利用分母有理化对C进行判断;根据二次根式的性质对D进行判断.
解答 解:A、原式=$\sqrt{2×3}$=$\sqrt{6}$,所以A选项的计算正确;
B、原式=5$\sqrt{2}$,所以B选项的计算正确;
C、原式=$\frac{1×\sqrt{2}}{\sqrt{2}×\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,所以C选项的计算正确;
D、原式=|$\sqrt{2}$-$\sqrt{3}$|=$\sqrt{3}$-$\sqrt{2}$,所以D选项的计算错误.
故选D.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
7.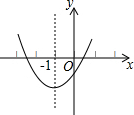 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )| A. | (l)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
5.一元二次方程两个根为1和3,那么这个方程为( )
| A. | x2+4x+3=0 | B. | x2+4x-3=0 | C. | x2-4x+3=0 | D. | x2-4x-3=0 |
12.下列不等式是一元一次不等式的是( )
| A. | 5>-2 | B. | x<0 | C. | x+y>0 | D. | x2+x+9≥0 |
6.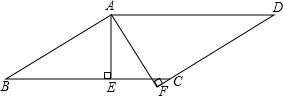 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )| A. | 60° | B. | 50° | C. | 70° | D. | 65° |