题目内容
17. 如图,△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BC2等于40.
如图,△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BC2等于40.
分析 由已知可求得AD的长,再根据勾股定理求得BD,BC的长,可得结果.
解答 解:∵AB=AC=10,BD⊥AC于D,CD=2,
∴AD=8,
∴在Rt△ADC中,BD=6,
在Rt△ADC中,BC=2$\sqrt{10}$,
∴BC2=40,
故答案为:40.
点评 本题考查了利用勾股定理解直角三角形的能力,先求BD的长是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
5. 如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
 如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )| A. | $\widehat{AC}=\widehat{BC}$ | B. | AE=EB | C. | CD平分∠ACB | D. | BA平分∠CBD |
12. 如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
 如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )
如图,一个圆形转盘被分成了6个圆心角都为60°的扇形,任意转动这个转盘一次,当转盘停止转动时,指针指向阴影区域的概率是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
9.下列说法不正确的有( )
①三内角之比是1:2:3的三角形是直角三角形;
②三内角之比为3:4:5的三角形是直角三角形;
③三边之比是3:4:5的三角形是直角三角形;
④三边a,b,c满足关系式a2-b2=c2的三角形是直角三角形.
①三内角之比是1:2:3的三角形是直角三角形;
②三内角之比为3:4:5的三角形是直角三角形;
③三边之比是3:4:5的三角形是直角三角形;
④三边a,b,c满足关系式a2-b2=c2的三角形是直角三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列不等式组无解的是( )
| A. | $\left\{\begin{array}{l}{x>-3}\\{x<2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥-1}\\{x<-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥4\frac{1}{2}}\\{x≤4\frac{1}{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤-3}\\{x<-4}\end{array}\right.$ |
 如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.
如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.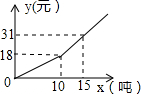 我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元.
我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元.