题目内容
【题目】如图,二次函数![]() (其中
(其中![]() )的图像与
)的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
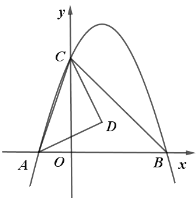
(1)点![]() 的坐标为 ,
的坐标为 ,![]()
![]() ;
;
(2)若![]() 为
为![]() 的外心,且
的外心,且![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,试探究抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
![]() 或
或![]()
【解析】
(1)令![]() ,结合点A在x轴的负半轴,即可得到点A、B的坐标;然后求出点C的坐标,得到
,结合点A在x轴的负半轴,即可得到点A、B的坐标;然后求出点C的坐标,得到![]() ,即可得到答案;
,即可得到答案;
(2)由点D是外心,则![]() ,得到
,得到![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,利用相似三角形的性质,即可得到答案;
,利用相似三角形的性质,即可得到答案;
(3)根据题意,可分为两种情况进行分析,分别求出每一种情况的坐标,即可得到答案.
解:(1)令![]() ,则
,则![]() ,
,
解得:![]() ,
,![]() .
.
![]() ,
,![]() .
.
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ;
;
(2)![]() 为
为![]() 的外心,
的外心,
![]() ,且
,且![]() .
.
![]() 为等腰直角三角形.
为等腰直角三角形.
![]() .
.
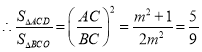 .
.
![]() ,
,
![]() .
.
(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() ,过程如下:
,过程如下:
![]() ,
,
![]() ,
,
![]() ,且抛物线的对称轴为直线
,且抛物线的对称轴为直线![]() .
.
作![]() 的外接圆
的外接圆![]() ,设
,设![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .
.
![]() 为
为![]() 的外心,
的外心,
![]() ,且
,且![]() 在
在![]() 上.
上.
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() .
.
易证![]() ,
,
![]() .
.
![]() 即为满足条件的一个点.
即为满足条件的一个点.
在![]() 轴上取点
轴上取点![]() ,易证
,易证![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
由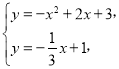
解得: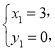 或
或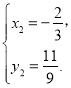
![]() .
.
综合上述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目