Question

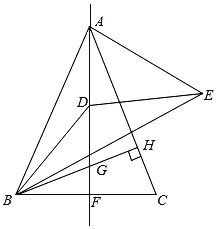
【题目】如图，在△ABC中，AB＝AC＝4，AF⊥BC于点F，BH⊥AC于点H．交AF于点G，点D在直线AF上运动，BD＝DE，∠BDE＝135°，∠ABH＝45°，当AE取最小值时，BE的长为_____．

Answer 1

【答案】2．

【解析】

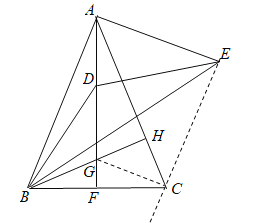
如图，连接CG，CE．证明△DBG∽△EBC，推出∠BGD＝∠BCE＝112.5°，推出∠ACE＝45°，推出点E的运动轨迹是直线EC，推出当AE⊥EC时，AE的值最小，再利用勾股定理求出BE即可．

如图，连接CG，CE．

∵BH⊥AC，

∴∠BHA＝90°，

∵∠ABH＝45°，

∴∠BAC＝45°，

∵AB＝AC，AF⊥BC，

∴∠BAF＝∠CAF＝22.5°，BF＝CF，

∴GB＝GC，

∴∠BGF＝∠CGF＝67.5°，

∴∠GBF＝∠GCF＝22.5°，

∵DB＝DE，∠BDE＝135°，

∴∠DBE＝∠DEB＝22.5°，

∴∠DBE＝∠GBC＝∠DEB＝∠GCF，

∴△DBE∽△GBC，

∴＝，

∴＝，

∵∠DBG＝∠EBC，

∴△DBG∽△EBC，

∴∠BGD＝∠BCE＝112.5°，

∵∠ACB＝67.5°，

∴∠ACE＝45°，

∴点E的运动轨迹是直线EC，

∴当AE⊥EC时，AE的值最小，最小值＝AC＝2，

此时∠BAE＝90°，BE＝＝＝2，

故答案为2．